Dominator 讲解及其相关性质的证明

前言

Dominator 的计算在编译器优化、程序分析等领域会用到，本文章将详细讲解 Dominator ，给出相关的定义，描述相关的性质，并给出性质的证明。

注 1：

本文中的图都是有限图，其节点和边的数量都是有限的，下文中不会再次说明。

注 2：

本文不包含多个 Dominator 算法的实现和正确性证明，具体原因请看 结语 ，但是我有用 Common Lisp 实现了 Purdom Dominator 算法、 Iterative Dominator 算法、 Cooper Dominator 算法、 Tarjan Dominator 算法，读者可以参考： cl-dominator 。

章节 1： Flow Graph, Dominator, Strict Dominator, Immediate Dominator, Dominator Tree 的定义及相关性质的证明

本文假设读者有图论相关的知识，故不会给出图论相关的定义。

首先，我们给出程序流图，即 Flow Graph 的定义，读者可能会有疑问，Flow Graph 不是很简单吗？一个节点 Entry 作为程序入口点，然后其他多个节点代表代码块（或者单条执行语句），节点间的连线代表可能的控制流（意思就是代码可能的走向），不就完事了？差不多是这样的，但是针对 Dominator 的计算（以及很多优化算法），我们额外需要一个 Flow Graph 具有一个性质，就是 Entry 可达每个节点，换句话来说，针对 Flow Graph 的每个节点 A ，必须存在一条从 Entry 到 A 的路径，这个性质的作用我们后面讲。

下面给出 Flow Graph 的定义：

定义 1.1 （ Flow Graph ）：

给定有向图 \( G(V, E) \) ，其中 \( V \) 为节点集， \( E \) 为边集，我们称 \( G \) 为 Flow Graph 当且仅当 \( G \) 满足：

1. 存在 唯一 一个名为 Entry 的节点。
2. 针对所有节点 \( A \in V \) ，要求 Entry 可达 \( A \) ，具体的，存在一条从 Entry 到\( A \) 的路径，路径的长度可为 0 ，特别的， Entry 本身也可达 Entry 。

我们把 Flow Graph 记为 \( G(V, E, \text{Entry}) \) 。

定义完毕。

类似的，读者可以额外要求 Flow Graph 具有唯一的出口点 Exit ，然后和 Entry 反过来，要求所有节点均可达 Exit （而不是 Exit 可达所有节点），这个性质对于计算 Post Dominator 来说有用，但是对于大部分计算 Dominator 的算法来说没用，故我们这里不对 Exit 节点有要求。虽然本文不讲解 Post Dominator ，但是读者在下面看完 Dominator 的定义后，很容易自己想出来 Post Dominator ，其对应的算法也刚好和 Dominator 是对称的，读者在掌握完 Dominator 的算法后，很容易自己想出来 Post Dominator 的算法。

现在我们可以给出 Dominator 的定义了：

定义 1.2 （ Dominator ）：

给定 Flow Graph \( G(V, E, \text{Entry}) \) 以及一个节点 \( A \in V \) ，我们称某个节点 \( D \in V \) 为 \( A \) 的 Dominator 当且仅当 \( D \) 满足：针对任意从 Entry 到 \( A \) 的路径 \( p = [x_1, x_2, \dots, x_n], x_1 = \text{Entry}, x_n = A \) ，均有 \( D \) 在路径 \( p \) 上，即 \( \exists 1 \leq i \leq n, x_i = D \) 。我们用记号 \( D \mathop{dom} A \) 表示 \( D \) 为 \( A \) 的 Dominator 。我们记节点 \( A \) 所有 Dominator 组成的集合为 \( \mathop{doms}(A) \) ，特别的，有 \( \forall B \in \mathop{doms}(A), B \mathop{dom} A \) 。

定义完毕。

从上述定义我们可以看出，一个节点 \( A \) 的 Dominator \( D \) 的关键属性在于，沿着任意路径从 Entry 到达 \( A \) ，都无法绕开 \( D \) ，很多优化算法可以利用该性质，比如我们要移动 \( A \) 内的某段代码到比较早的地方执行，移动到哪个节点呢？这个节点明显得满足：任意从 Entry 到达 \( A \) 的路径，都得经过该节点，不然原本到达 \( A \) 必执行的代码，在移动代码后会变得不一定执行，可能会改变程序的语义，此时 Dominator 就是其中一个满足上述性质，可以考虑的候选节点（当然，为了移动代码后保持程序语义，这个节点还得满足很多其他性质）。

容易看出， Dominator 具有一个平凡的性质，即任意节点自身就是自身的其中一个 Dominator ：

定理 1.1 （自身是自身的 Dominator ）：

给定 Flow Graph \( G(V, E, \text{Entry}) \) 以及一个节点 \( A \in V \) ，我们有 \( A \mathop{dom} A \) 。

证明：

针对任意路径\( p = [x_1, x_2, \dots, x_n], x_1 = \text{Entry}, x_n = A \) ，由 \( x_n = A \) 可得， \( A \) 在路径 \( p \) 上，综上，由 Dominator 的定义可得， \( A \) 为 \( A \) 的 Dominator ，即 \( A \mathop{dom} A \) 。

证毕。

针对 \( A \mathop{dom} A \) ，我们称 \( A \) 为 \( A \) 的平凡 Dominator ，有时候我们想排除平凡 Dominator 这种情况，比如给定 \( D \) 为 \( A \) 的 Dominator ，我们想表达 \( D \) 不能是 \( A \) ，就得写成 \( D \mathop{dom} A, D \neq A \) ，不方便，为此，我们引入如下定义：

定义 1.3 （ Strict Dominator ）：

给定 Flow Graph \( G(V, E, \text{Entry}) \) 以及节点 \( D, A \in V \) 满足 \( D \mathop{dom} A \) ，我们称 \( D \) 为 \( A \) 的 Strict Dominator 当且仅当 \( D \mathop{dom} A \) 且 \( D \neq A \) ，记为 \( D \mathop{sdom} A \) 。类似 Dominator ，我们记节点 \( A \) 所有 Strict Dominator 组成的集合为 \( \mathop{sdoms}(A) \) ，特别的，有 \( \forall B \in \mathop{sdoms}(A), B \mathop{sdom} A \) 。

定义完毕。

节点 Entry 比较特别，它的 Dominator 有且仅有它本身，且它是所有节点的 Dominator ，如下：

定理 1.2 （ Entry 的 Dominator 仅有自己， Entry 是所有节点的 Dominator ）：

给定 Flow Graph \( G(V, E, \text{Entry}) \) ，则 \( G \) 的入口点 Entry 满足：

1. \( \mathop{doms}(\text{Entry}) = \{ \text{Entry} \} \)
2. \( \forall A \in V, \text{Entry} \mathop{dom} A \)

证明 1 ：

由 定理 1.1 ，可得 \( \text{Entry} \mathop{dom} \text{Entry} \) ，从而 \( \text{Entry} \in \mathop{doms}(\text{Entry}) \) ，我们证明了 \( \mathop{doms}(\text{Entry}) \) 有 Entry 这个元素，还得证明它仅有这个元素，具体的，需要证明 \( \forall A \in V, A \neq \text{Entry} \) ， \( A \) 不是 Entry 的 Dominator ： \( \forall A \in V, A \neq \text{Entry} \) ，令路径 \( p = \text{Entry} \) ，则由 \( A \neq \text{Entry} \) ，可得路径 \( p \) 不包含 \( A \) ，于是有 \( A \) 不是 Entry 的 Dominator 。

综上，有 \( \mathop{doms}(\text{Entry}) = \{ \text{Entry} \} \) 。

证明 2 ：

由于所有路径的起点都是 Entry ，因此显然有 \( \forall A \in V, \text{Entry} \mathop{dom} A \) 。

证毕。

符合直觉的， Dominator 关系具有传递性，如下：

定理 1.3 （ Dominator 关系具有传递性）：

给定 Flow Graph \( G(V, E, \text{Entry}) \) 以及节点 \( A, B, C \in V \) 满足 \( A \mathop{dom} B, B \mathop{dom} C \) ，则有 \( A \mathop{dom} C \) 。

证明：

给定任意从 Entry 到 \( C \) 的路径 \( p = [x_1, x_2, \dots, x_n], x_1 = \text{Entry}, x_n = C \) ，我们需要证明 \( \exists 1 \leq i \leq n, x_i = A \) ，由 \( B \mathop{dom} C \) ，可得 \( \exists 1 \leq i_1 \leq n, x_{i_1} = B \) ，令 \( p_1 = [x_1, x_2, \dots, x_{i_1}] \) ，这里 \( p_1 \) 为从 Entry 到 \( B \) 的路径，由 \( A \mathop{dom} B \) ，可得 \( \exists 1 \leq i \leq i_1, x_{i} = A \) ，这里同时由 \( i_1 \leq n \) 可得 \( 1 \leq i \leq n \) ，至此，我们证明了 \( \exists 1 \leq i \leq n, x_i = A \) ，由定义可得 \( A \mathop{dom} C \) 。

证毕。

Dominator 关系也符合反对称性，为了证明这点，我们先引入简单路径的概念：

定义 1.4 （简单路径）：

给定任意有向图 \( G(V, E) \) ，给定 \( G \) 的一个路径 \( p = [x_1, x_2, \dots, x_n] \) ，我们称 \( p \) 为简单路径当且仅当 \( \forall 1 \leq i < j \leq n \) ，除非 \( i = 1, j = n \) ，不然有 \( x_i \neq x_j \) ，也就是只允许路径上的第一个和最后一个节点相同，其他节点均不同。

定义完毕。

特别的，给定任意路径 \( p = [x_1, x_2, \dots, x_n], x_1 = A, x_n = B \) ，该路径从 \( A \) 出发到达 \( B \) ，如果 \( p \) 不是简单路径，我们都可以给它简化成等价的简单路径，这里路径等价的定义如下：

定义 1.5 （路径等价）：

给定任意有向图 \( G(V, E) \) ，给定 \( G \) 的两个路径 \( p = [x_1, x_2, \dots, x_{n_1}], q = [y_1, y_2, \dots, y_{n_2}] \) ，我们称 \( p \) 和 \( q \) 等价当且仅当 \( x_1 = y_1, x_{n_1} = y_{n_2} \) ，记为 \( p \cong q \) ，换句话来说，两路径等价，当且仅当它们从同一节点出发到达相同的终点。

定义完毕。

路径等价明显是一个等价关系，如下：

定理 1.4 （路径等价为等价关系）：

路径等价关系满足自反性、对称性、传递性。

证明：

证明比较简单，这里省略。

证毕。

现在我们证明任意路径都可以简化成一个等价的简单路径：

定理 1.5 （路径均可以简化成等价的简单路径）：

给定任意有向图 \( G(V, E) \) ，给定 \( G \) 的一个路径 \( p = [x_1, x_2, \dots, x_n] \) ，则存在简单路径 \( q \) 满足 \( q \cong p \) 。

证明：

如果 \( p \) 已经是简单路径了，则 \( p \cong p \) ，完毕，如果 \( p \) 不是简单路径，则 \( \exists 1 \leq i < j \leq n \)，满足 \( x_i = x_j \) 且 （ \( i \neq 1 \) 或 \( j \neq n \) ） ，接下来分情况讨论：

1. 如果 \( j \neq n \) ，即 \( x_j \) 不是路径的最后一个节点，则有 \( j < n, j + 1 \leq n \) ，因此 \( x_{j + 1} \) 仍然是路径的一个节点，此时我们构造新路径 \( p' = [x_1, x_2, \dots, x_i, x_{j + 1}, \dots, x_n] \) ，即原本到 \( x_i \) 后，是接着走到 \( x_{i + 1} \) ，现在改成直接走到 \( x_{j + 1} \) ，易得 \( p' \cong p \) ，同时 \( p' \) 的路径长度严格比 \( p \) 小，因为我们至少去掉了一个节点 \( x_j \) 。
2. 如果 \( j = n \) ，即 \( x_j \) 是路径的最后一个节点，则我们构造新路径 \( p' = [x_1, x_2, \dots, x_i] \) ，易得 \( p' \cong p \) ，同时 \( p' \) 的路径长度严格比 \( p \) 小，因为我们至少去掉了一个节点 \( x_j \) 。

综上，如果 \( p \) 不是简单路径，则我们可以构造一条更短的、等于与 \( p \) 的路径 \( p' \)，这里如果 \( p' \) 是简单路径，则我们已经得到了我们要的简化路径，如果 \( p' \) 仍然不是简单路径，则我们可以进一步针对 \( p' \) 重复上面的步骤，得到一个更短的等价路径。如此重复，我们要么中途得到一个简单路径，目的达成，要么最终得到一个长度为 0 、仅有一个节点的等价路径 \( p'' = [x_1] \) ，这里 \( p'' \) 显然是简单路径且 \( p'' \cong p \) （由路径等价关系的对称性和传递性可以得到），也达成我们的目的了。

证毕。

现在，我们可以去证明 Dominator 关系的反对称性了：

定理 1.6 （ Dominator 关系具有反对称性）：

给定 Flow Graph \( G(V, E, \text{Entry}) \) 以及节点 \( A, B \in V \) 满足 \( A \mathop{dom} B, B \mathop{dom} A \) ，则有 \( A = B \) 。

证明：

假设 \( A \neq B \) ，由 Flow Graph 的定义，可得 Entry 可达 \( A \) ，于是存在路径 \( p = [x_1, x_2, \dots, x_n], x_1 = \text{Entry}, x_n = A \) ，根据 定理 1.5 可得，存在一个简单路径 \( q = [y_1, y_2, \dots, y_{n_1}], y_1 = \text{Entry}, y_{n_1} = A \)，由 \( B \mathop{dom} A \) 得， \( \exists 1 \leq i \leq n_1, y_i = B \) ，这里由于 \( A \neq B \) ，因此 \( i < n_1 \) ，针对路径 \( q' = [y_1, y_2, \dots, y_i] \) ，由 \( A \mathop{dom} B \) 得， \( \exists 1 \leq j \neq i, y_j = A \) ，同理由于 \( A \neq B \) ，因此 \( j < i \) ，可得\( y_j = y_{n_1} = A \) ，而简单路径除首尾节点外，其他节点均不能相同，分情况讨论：

1. 如果 \( j = 1 \) ，此时 \( y_j, y_{n_1} \) 分别为路径 \( q \) 首尾节点，可以相同，但 \( A = y_j = y_1 = \text{Entry} \) ，于是 \( B \mathop{dom} (A = \text{Entry}) \) ，加上 \( A \neq B \) ，可得 \( B \neq \text{Entry} \) ，这意味着 \( \mathop{doms}(\text{Entry}) \neq \{ \text{Entry} \} \) ，和 定理 1.2 的 1 矛盾。
2. 如果 \( j \neq 1 \) ，此时 \( y_j, y_{n_1} \) 不是路径 \( q \) 的首尾节点，不能相同，这和 \( y_j = y_{n_1} = A \) 矛盾。

综上，所有情况均矛盾，可得假设不成立，有 \( A = B \) 。

证毕。

由上述定理，我们可以看到要求 Flow Graph 的 Entry 可达所有节点的其中一个作用，假设不要求 Entry 可达所有节点，则上述定理不成立，例子如下：

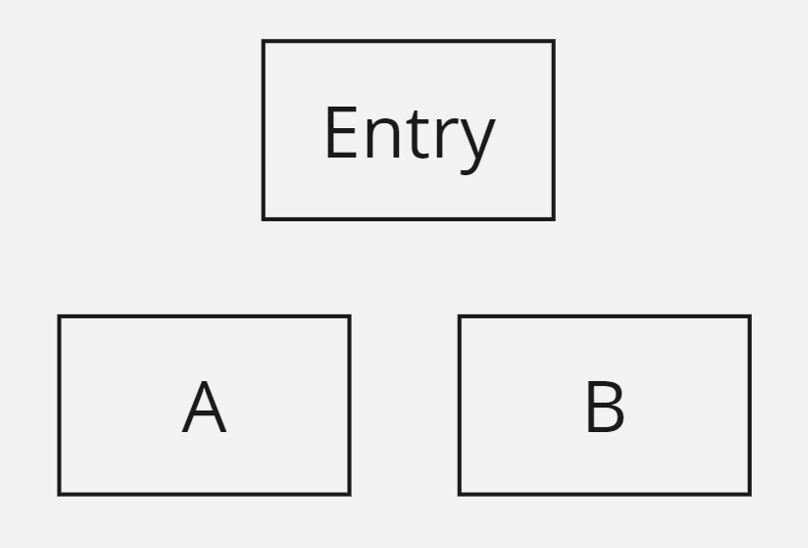
上图没有任何边， Entry 不可达 A 和 B ， 按 Dominator 的定义，易得 \( A \mathop{dom} B, B \mathop{dom} A \) ，但 \( A \neq B \) 。

Dominator 还有一个非常有用的性质，该性质确保了所有节点之间的 Dominator 关系可以通过树的形式呈现出来，如下（我不知道在数学领域，该类型的性质一般取什么名字，故我没有给该定理取名字）：

定理 1.7 ：

给定 Flow Graph \( G(V, E, \text{Entry}) \) 以及节点 \( A, B, C \in V \) 满足 \( A \mathop{dom} C, B \mathop{dom} C \) ，则有 \( A \mathop{dom} B \) 或 \( B \mathop{dom} A \) 。

证明：

如果 \( A = B \) ，则直接有 \( A \mathop{dom} B \) 。

如果 \( A \neq B \) ，此时假设 \( A, B \) 互相都不是对方的 Dominator （注：下面证明中，最好自己想象或者画下图，最终目标在于证明 \( B \) 不是 \( C \) 的 Dominator ，矛盾），此时由 \( A \mathop{dom} C, B \mathop{dom} C \) 可得 \( A \neq C, B \neq C \) ，由 \( B \) 不是 \( A \) 的 Dominator ，可得存在从 Entry 到 \( B \) 不经过 \( A \) 的路径 \( p_1 = [x_1, x_2, \dots, x_{n_1}], x_1 = \text{Entry}, x_{n_1} = B, \forall 1 \leq i \leq n_1, x_i \neq A \) ，易得 \( B \) 可达 \( C \) （这点容易由 Entry 可达 \( C \) 以及 \( B \mathop{dom} C \) 证出来），与此同时用 定理 1.5 ，可得存在简单路径 \( p_2 = [y_1, y_2, \dots, y_{n_2}], y_1 = B, y_{n_2} = C \)，特别的，有 \( \forall 2 \leq i \leq n_2 - 1, y_i \neq B \) ，即 \( p_2 \) 中间没有再次经过 \( B \) 节点，令 \( p_3 = [x_1, x_2, \dots, x_{n_1}, y_2, \dots, y_{n_2}] \) ，有 \( p_3 \) 为从 Entry 到 \( C \) 经过 \( B \) 的路径，此时由 \( A \mathop{dom} C \) ，可得 \( p_3 \) 中也必须包含 \( A \) 节点，而 \( \forall 1 \leq i \leq n_1, x_i \neq A \) ， 即路径 \( p_3 \) 的前半段不包含节点 \( A \) ，因此 \( A \) 只能在 \( p_3 \) 的后半段，即 \( \exists 2 \leq i_1 \leq n_2, y_{i_1} = A \) ，于是这里得到了一条从 \( A \) 到 \( C \) 的路径 \( p_4 = [y_{i_1}, y_{i_1 + 1}, \dots, y_{n_2}] \) ，加上前面得到的 \( \forall 2 \leq i \leq n_2 - 1, y_i \neq B \) 以及 \( B \neq C \) ，可得 \( p_4 \) 不包含节点 \( B \) ，也就是说 \( p_4 \) 为从 \( A \) 到 \( C \) 不经过 \( B \) 的路径。接下来我们准备构造一条绕过 \( B \) 直达 \( C \) 的路径，由 \( B \) 不是 \( A \) 的 Dominator ，可得存在 从 Entry 到 \( A \) 不经过 \( B \) 的路径 \( p_5 = [z_1, z_2, \dots, z_{n_3}], z_1 = \text{Entry}, z_{n_3} = A, \forall 1 \leq i \leq n_3, z_i \neq B \) ，将该路径和前面得到的从 \( A \) 到 \( C \) 不经过 \( B \)的路径 \( p_4 \) 拼接在一起，得到一条从 Entry 到 \( C \) 不经过 \( B \) 的路径 \( p_6 = [z_1, z_2, \dots, z_{n_3}, y_{i_1 + 1}, \dots, y_{n_2}] \) ，这和 \( B \mathop{dom} C \) 矛盾，因此假设不成立，有 \( A \mathop{dom} B \) 或 \( B \mathop{dom} A \) 。

证毕。

由上述定理，我们可以看到要求 Flow Graph 的 Entry 可达所有节点的另外一个作用，假设不要求 Entry 可达所有节点，则上述定理不成立，进而所有节点之间的 Dominator 关系就不能通过树的形式呈现出来（一个非常有用的性质），例子如下：

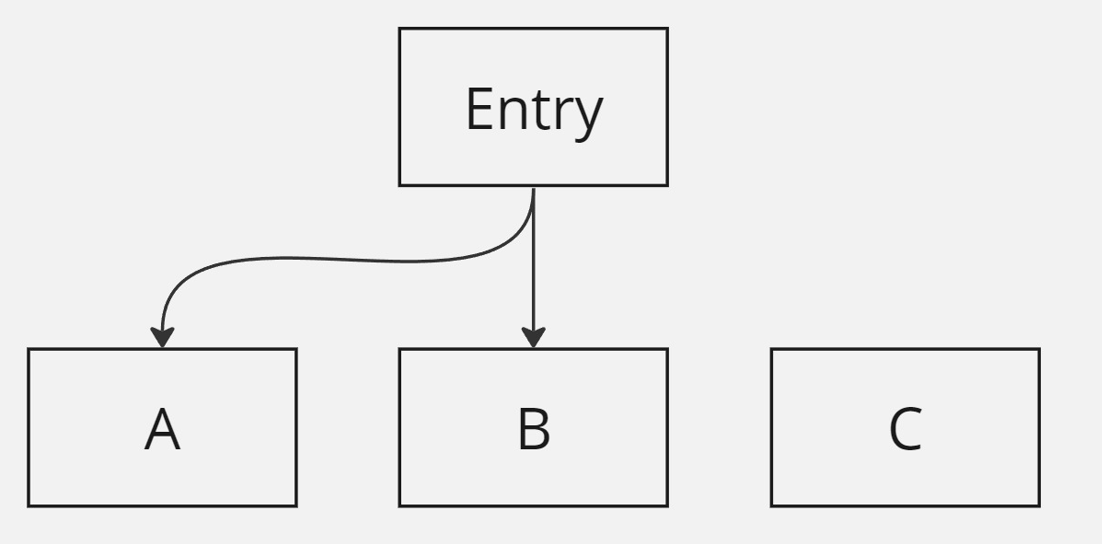
上图中， \( A \mathop{dom} C, B \mathop{dom} C \) ，但是 \( A, B \) 互相都不是对方的 Dominator 。

上面说了，上述定理确保了所有节点之间的 Dominator 关系可以通过树的形式呈现出来，为什么呢？思考下，如果你要将所有节点之间的 Dominator 关系通过树的形式呈现出来，那你就需要决定，谁是谁的父节点？孩子节点不用决定，因为父节点关系决定了，对应的孩子节点关系也就自然而然出来了。自然的，我们会想说，如果节点 \( A \mathop{dom} C \) ，则让 \( A \) 作为 \( C \) 的父节点或者祖先节点，也就是祖先节点为孙子节点的 Dominator ，或者反过来，让 \( C \) 作为 \( A \) 的父节点或者祖先节点，这样就是孙子节点为祖先节点的 Dominator ，我们先考虑第一种做法，即让 \( A \) 作为 \( C \) 的父节点或者祖先节点，之后再考虑另一种做法可不可行。

考虑 \( A \mathop{dom} C, B \mathop{dom} C \) 的情况，并且假设有且仅有 \( A, B \) 是 \( C \) 的 Dominator ，我们等等再考虑有三个及以上的节点为 \( C \) 的 Dominator 的情况，这里 \( A, B \) 都是 \( C \) 的 Dominator ，都要作为 \( C \) 的父节点或者祖先节点，但父节点只能有一个，谁作为父节点呢？在上述定理成立的情况下，我们知道 \( A, B \) 其中一个会是另一个的 Dominator ，因此很好决定，如果是 \( A \mathop{dom} B \) ，则 \( B \) 作为 \( C \) 的父节点， \( A \) 作为 \( B \) 的父节点就行，很自然，反之，如果是 \( B \mathop{dom} A \) ，则 \( A \) 作为 \( C \) 的父节点， \( B \) 作为 \( A \) 的父节点就行。如果上述定理不成立呢？则有可能会存在 \( A, B \) 互相不是对方的 Dominator 的情况，这时候，我们无法决定 \( A, B \) 谁作为 \( C \) 的父节点的“优先级”比较高，进而所有节点之间的 Dominator 关系无法通过树的形式呈现出来。

我们等等再考虑有三个及以上的节点为 \( C \) 的 Dominator 的情况，现在继续回去考虑之前说的另外一种做法，即反过来，让孙子节点为祖先节点的 Dominator ，也就是让 \( C \) 作为 \( A, B \) 的父节点或者祖先节点，这种情况其实和上面的讨论是对称的（但是还是有点不一样的），类似上面，我们这里假设有且仅有 \( A, B \) 是 \( C \) 的 Dominator ，则和前面的讨论一样， \( C \) 的孩子节点只能有一个， \( A, B \) 谁作为 \( C \) 的孩子节点的“优先级”更高点呢？同上，如果上述定理不成立，则我们也无法决定 \( A, B \) 的“优先级”，进而所有节点之间的 Dominator 关系无法通过树的形式呈现出来。但是，即使上述定理成立，则该做法仍然不可行，这里考虑另外一个 Dominator 关系的例子： \( D \mathop{dom} E, D \mathop{dom} F \) ，且 \( E, F \) 互相不是对方的 Dominator （读者很容易自己画出来对应的图，这种情况是可能的），这里问题就出现了， \( E, F \) 谁作为 \( C \) 的父节点？不知道啊， \( E, F \) 之间没有 Dominator 关系，无法决定“优先级”，所以这个做法不可行。

既然第二个做法不可行，那我们采取第一个做法，继续考虑前面说到的，有三个及以上的节点为 \( C \) 的 Dominator 的情况，这里具体怎么决定节点之间的父子关系？假设 \( A, B, D \) 均为 \( C \) 的 Dominator ，我们考虑谁作为 \( C \) 的父节点， \( A \) 吗？你会说，那得看 \( A \) 是否是 \( B \) 的 Dominator ，如果是的话，则 \( A \) 在树中应该在 \( B \) （以及 \( C \) ） 的上面，此时应该优先考虑 \( B \) 作为 \( C \) 的 Dominator ，同理还得考虑 \( A \) 是否是 \( D \) 的 Dominator ，以及 \( B, D \) 之间的 Dominator 关系，等等，一般的，一个节点 \( D \) 要想是另外一个节点 \( E \) 的父节点，那它得是离 \( E \) “最近”的 Dominator ，这里”最近“的意思就是，如果有其他任意节点 \( X \mathop{dom} E \) ，那必须得有 \( X \mathop{dom} D \) ，也就是 \( D \) 在树中应该在 \( X \) 的下面，总的来说， \( D \) 得是 \( E \) 所有 Dominator 中“最下面”的那一个，为此，我们定义 Immediate Dominator 来严格表达这“最近”的 Dominator 的概念，如下：

定义 1.6 （ Immediate Dominator ）：

给定 Flow Graph \( G(V, E, \text{Entry}) \) 以及一个节点 \( A \in V \) ，我们称某个节点 \( D \in V \) 为 \( A \) 的 Immediate Dominator 当且仅当 \( D \) 满足：

1. \( D \mathop{sdom} A \) （这里用 \( \mathop{sdom} \) 是为了确保 \( D \neq A \) ）
2. \( \forall D' \in V \) ，如果 \( D' \mathop{sdom} A \) ，则 \( D' \mathop{dom} D \) 。

记为 \( D \mathop{idom} A \) 。

定义完毕。

由定理 7，易得上述定义的第二点等价于 没有 任何节点 \( D' \in V \) 满足 \( D \mathop{sdom} D' \mathop{sdom} A \) ，这种说法应该会比较满足读者对“最近” Dominator 这个概念的理解，下面是具体定理的描述和证明：

定理 1.8 （ Immediate Dominator 的另一个等价性描述 ）：

给定 Flow Graph \( G(V, E, \text{Entry}) \) 以及两个节点 \( D, A \in V \) ，则 \( D \mathop{idom} A \) 当且仅当 \( D, A \) 满足以下两点：

1. \( D \mathop{sdom} A \)
2. 没有 任何节点 \( D' \in V \) 满足 \( D \mathop{sdom} D' \mathop{sdom} A \) 。

证明：

必要性：

如果 \( D \mathop{idom} A \) ，则有：

1. \( D \mathop{sdom} A \)
2. \( \forall D' \in V \) ，如果 \( D' \mathop{sdom} A \) ，则 \( D' \mathop{dom} D \) (1) 。

我们得证明：

1. \( D \mathop{sdom} A \)
2. 没有 任何节点 \( D' \in V \) 满足 \( D \mathop{sdom} D' \mathop{sdom} A \) (2) 。

这里第一点已经成立，还得证明第二点，假设第二点不成立，即存在节点 \( D' \in V \) 满足 \( D \mathop{sdom} D' \mathop{sdom} A \) ，则由 \( D' \mathop{sdom} A, D \mathop{sdom} A \) 以及 定理 1.7 可得， \( D' \mathop{sdom} D \) 或 \( D \mathop{sdom} D' \) ，分情况讨论：

1. 如果 \( D' \mathop{sdom} D \) ，则由 (2) 处的 \( D \mathop{sdom} D' \) 以及 定理 1.6 ，可得 \( D' = D \) ，而这与 \( D' \mathop{sdom} D \) 矛盾（因为 Strict Dominator 关系要求两者不相等 ）。
2. 如果 \( D \mathop{sdom} D' \) ，则由 (1) 处的 \( D' \mathop{sdom} D \) 以及 定理 1.6 ，可得 \( D' = D \) ，也与 \( D' \mathop{sdom} D \) 矛盾。

综上，所有情况均矛盾，可得假设不成立，结论是上述的第二点成立。

充分性：

如果 \( D, A \) 满足以下两点：

1. \( D \mathop{sdom} A \)
2. 没有 任何节点 \( D' \in V \) 满足 \( D \mathop{sdom} D' \mathop{sdom} A \) (3) 。

则我们要证明

1. \( D \mathop{sdom} A \)
2. \( \forall D' \in V \) ，如果 \( D' \mathop{sdom} A \) ，则 \( D' \mathop{dom} D \) 。

这里第一点已经成立，还需要证明第二点，假设第二点不成立，即存在节点 \( D' \in V \) 满足 \( D' \mathop{sdom} A \) 且 \( D' \) 不是 \( D \) 的 Dominator ，则由 \( D' \mathop{sdom} A, D \mathop{sdom} A \) 以及 定理 1.6 ，可得 \( D' \mathop{sdom} D \) 或 \( D \mathop{sdom} D' \) ，又 \( D' \) 不是 \( D \) 的 Dominator ，因此可排除 \( D' \mathop{sdom} D \) ，得 \( D \mathop{sdom} D' \) ，于是有 \( D \mathop{sdom} D' \mathop{sdom} A \) ，这和 (3) 矛盾，因此假设不成立，结论是上述的第二点成立。

证毕。

符合直觉的，一个节点的 Immediate Dominator 就是它在 Dominator Tree 中的父节点（我们还没有定义 Dominator Tree ， 这里 Dominator Tree 指的是所有节点间 Dominator 关系对应的树形式呈现 ），与之而来的，我们会产生疑问，是否每个节点都一定会有 Immediate Dominator 呢？有的话，是不是唯一的呢（显然一定要是唯一的，不然树不允许有多个父节点）？作为树，还得有根节点，根节点显然应该是 Entry ，那 Entry 符不符合作为根节点的需求？上述疑问是接下来我们要讨论、证明的东西。

首先第一个简单的结论，如下：

定理 1.9 （ Entry 没有 Immediate Dominator ）：

给定 Flow Graph \( G(V, E, \text{Entry}) \) ，它的入口点 Entry 没有 Immediate Dominator 。

证明：

由 定理 1.2 的 1 得，\( \mathop{doms}(\text{Entry}) = \{ \text{Entry} \} \) ，而 Entry 的 Immediate Dominator 不能等于 Entry 本身，但是又没有其他候选者，因此 Entry 没有 Immediate Dominator 。

证毕。

下一个结论， Immediate Dominator 的存在以及唯一性：

定理 1.10 （ 非 Entry 节点均有唯一的 Immediate Dominator ）：

给定 Flow Graph \( G(V, E, \text{Entry}) \) ，针对所有节点 \( A \in V, A \neq \text{Entry} \) ，我们有 \( A \) 有且仅有一个 Immediate Dominator 。

证明：

先证 Immediate Dominator 的存在性，假设 \( A \) 没有 Immediate Dominator ，由 \( A \neq \text{Entry} \) ，可得 \( A \) 至少有 Entry 这个 Strict Dominator ，而 Immediate Dominator 的其中一个要求就是它得是 Strict Dominator ，此时由 \( A \) 没有 Immediate Dominator ，可得在 \( A \) 的众多 Strict Dominator 中，没有一个是满足 定理 1.8 中 Immediate Dominator 的第二个要求的，也就是，针对任意 \( D \in \mathop{sdoms}(A) \) ，均存在另外一个 \( D' \in \mathop{sdoms}(A) \) 满足 \( D \mathop{sdom} D' \mathop{sdom} A \) (1) ，记 \( \mathop{sdoms}(A) = \{ D_1, D_2, \dots, D_n \} \) ，令 \( i_1 = 1 \) ，由 (1) 得，存在 \( D_{i_2} \in \mathop{sdoms}(A) \) 满足 \( (D_{i_1} = D_1) \mathop{sdom} D_{i_2} \mathop{sdom} A \) ，再由 (1) 以及 \( D_{i_2} \mathop{sdom} A \) 可得存在节点 \( D_{i_3} \) 满足 \( D_{i_1} \mathop{sdom} D_{i_2} \mathop{sdom} D_{i_3} \mathop{sdom} A \) ，以此重复共 \( n + 1 \) 次，得到 \( D_{i_1} \mathop{sdom} D_{i_2} \dots \mathop{sdom} D_{i_{n + 1}} \mathop{sdom} A \) ，由于 \( \mathop{sdoms}(A) \) 只有 \( n \) 个节点，这意味着 \( D_{i_1}, D_{i_2}, \dots, D_{i_{n + 1}} \) 中一定至少有两个是重复的节点，即 \( \exists 1 \leq j_1 < j_2 \leq n + 1, D_{i_{j_1}} = D_{i_{j_2}} \) ，但是 \( D_{i_{j_1}} \mathop{sdom} D_{i_{j_1} + 1} \dots \mathop{sdom} D_{i_{j_2}} \) ，由传递性，可得 \( D_{i_{j_1}} \mathop{sdom} D_{i_{j_2}} \) ，而 Strict Dominator 关系意味着 \( D_{i_{j_1}} \neq D_{i_{j_2}} \) ，这和 \( D_{i_{j_1}} = D_{i_{j_2}} \) 矛盾，因此假设不成立，结论是 \( A \) 有 Immediate Dominator 。

最后证明唯一性，如果 \( D \mathop{idom} A, D' \mathop{idom} A \) ，则由 定理 1.7 ，可得 \( D \mathop{dom} D' \) 或 \( D' \mathop{dom} D \) ，不妨设 \( D \mathop{dom} D' \) （这里“不妨设”的意思是，其他几种情况，比如这里的 \( D' \mathop{dom} D \) ，和我们接下来要讨论的情况同理，因此我们省略其他几种情况的讨论） ，此时假设 \( D \neq D' \) ，则有 \( D \mathop{sdom} D' \mathop{idom} A \) ，这和 \( D \mathop{idom} A \) 矛盾（ 定理 1.8 的第二点 ） ，因此假设不成立，有 \( D = D' \) 。

证毕。

由于非 Entry 的 Immediate Dominator 是存在且唯一的，因此我们可以引入如下的记号：

记号 1.1 （ Immediate Dominator 的记号）：

给定 Flow Graph \( G(V, E, \text{Entry}) \) ，针对所有节点 \( A \in V, A \neq \text{Entry} \) ，我们记 \( A \) 唯一的 Immediate Dominator 为 \( \text{IDOM}(A) \) 。

定义记号完毕。

终于，我们现在可以证明所有节点之间的 Dominator 关系可以通过树的形式呈现出来了，在此之前，我们先定义下 Dominator Tree ，这里提前称它为 Tree ，严格来说，应该得到之后我们证明了它是树，才能称它为 Dominator Tree ，不然严格点，应该先称为 Dominator Graph ，之后证明了它是树，再给别称 Dominator Tree ，这里就不这么麻烦了。

定义 1.7 （ Dominator Tree ）：

给定 Flow Graph \( G(V, E, \text{Entry}) \) ，构造图 \( G'(V, E') \) ，这里 \( G' \) 的节点集和 \( G \) 一样都是 \( V \) ，而 \( E' = \{ (A, B) \mid A \in V, B \in V, A \mathop{idom} B \} \) ，即如果 \( A \) 是 \( B \) 的 Immediate Dominator ，则在 \( G' \) 中由 \( A \) 到 \( B \) 将两者连起来，这里称 \( G' \) 为 \( G \) 的 Dominator Tree，记为\( \mathop{DT}(G) \) 。

定义完毕。

好了，可以证明 Dominator Tree 真的是 Tree 了：

定理 1.11 （ Dominator Tree 真的是 Tree ， Dominator 关系可以通过树的形式呈现出来）：

给定 Flow Graph \( G(V, E, \text{Entry}) \) ，则 \( \mathop{DT}(G) \) 为树。

证明：

证明 \( \mathop{DT}(G) \) 为树，我们得证明 3 点：

1. 有一个节点 \( R \) 的入度为 0 ，这个节点是树的根节点。
2. 除 \( R \) 外，其他节点的入度均为 1 。
3. \( R \) 在 \( \mathop{DT}(G) \) 中可达任何节点。

注：这里第 3 点很重要，是用来确保 \( \mathop{DT}(G) \) 中无环的，举个例子，假设我们不确保第 3 点成立，则你可以构造一个图，该图包含一圈的节点 \( A \to B \to C \to A \) ，以及一个不与任何节点相连的“根节点” \( R \) ，该图满足前 2 点，但是它不是树。

由 定理 1.9 ，可得 Entry 没有 Immediate Dominator ，进而根据 Dominator Tree 的定义，不会有边连向 Entry ，令 \( R = \text{Entry} \) ，有 \( R \) 的入度为 \( 0 \) 。

由 定理 1.10 ，可得除 \( R \) 外，所有节点 \( A \) 均有且仅有一个 Immediate Dominator ，进而根据 Dominator Tree 的定义，可得仅有一条边连向 \( A \) ，即 \( A \) 的入度为 1 。

由 \( \mathop{DT}(G) \) 的定义，我们知道 \( \mathop{DT}(G) \) 的节点集和 \( G \) 一样都是 \( V \) ，故我们得证明\( \forall A \in V \) ， \( R \) 在 \( \mathop{DT}(G) \) 中可达 \( A \) ： \( \forall A \in V \) ，我们定义一系列节点 \( P_1, P_2, \dots \) ，令 \( P_1 = A \) ，归纳假设当 \( i = k \) 时， \( P_i \) 已定义，当 \( i = k + 1 \) 时，如果 \( P_k = R \) ，则令 \( P_i = P_k = R \) ，如果 \( P_k \neq R \) ，则 \( P_k \) 有唯一的 Immediate Dominator ，此时令 \( P_i = \text{IDOM}(P_k) \) ，定义系列节点完毕，接下来分情况讨论：

1. 如果 \( \exists i \geq 1 \) 满足 \( P_i = R \) ，则我们取 \( i_0 \) 为满足条件的最小下标，即 \( i_0 = \min \{ i \mid i \geq 1 \text{且} P_i = R \} \) ，则易得 \( \forall 1 \leq i < j \leq i_0, P_i \neq P_j \) ，进而可得 \( P_{i_0} \mathop{idom} P_{i_0 - 1} \dots \mathop{idom} P_{1} \) ，这意味着 \( \forall 1 \leq i < i_0, (P_i, P_{i + 1}) \) 为 \( \mathop{DT}(G) \) 的边，可得 \( R \) 在 \( \mathop{DT}(G) \) 中可达 \( P_1 = A \) ，特别的，当 \( i_0 = 1 \) 时， \( P_{i_0} = P_1 = R = A \) ，此时也有 \( R \) 在 \( \mathop{DT}(G) \) 中可达 \( A \) 。
2. 如果 \( \forall i \geq 1 \) 均有 \( P_i \neq R \) ，则由于 \( V \) 是有限集，此时 \( P_1, P_2, \dots \) 中必然存在重复节点，即 \( \exists 1 \leq i_0 < j_0, P_{i_0} = P_{j_0}, P_{i_0} \neq R, P_{j_0} \neq R \) ，易得 \( P_{j_0} \mathop{idom} P_{j_0 - 1} \dots \mathop{idom} (P_{i_0} = P_{j_0}) \) ，由传递性，可得 \( P_{j_0} \mathop{idom} P_{j_0} \) ，这意味着 \( P_{j_0} \mathop{sdom} P_{j_0} \) ，进而有 \( P_{j_0} \neq P_{j_0} \) ，矛盾，因此这种情况是不可能的。

综上，所有情况下均有 \( R \) 在 \( \mathop{DT}(G) \) 中可达 \( A \) 。

至此可得， \( \mathop{DT}(G) \) 为树。

证毕。

作为 Dominator Tree 为树的其中一个好处：针对任意节点 \( A \neq \text{Entry} \) ，我们可以不记录它所有 Dominator 的集合 \( \mathop{doms}(A) \) ，而仅记录它的 Immediate Dominator \( \text{IDOM}(A) \) ，然后从 \( A \) 开始顺着 Dominator Tree 往上走，直接走到 Entry ，记录经过的所有节点（包括 \( A \) ），这样就能还原出所有 \( \mathop{doms}(A) \) 中的元素，举个例子：

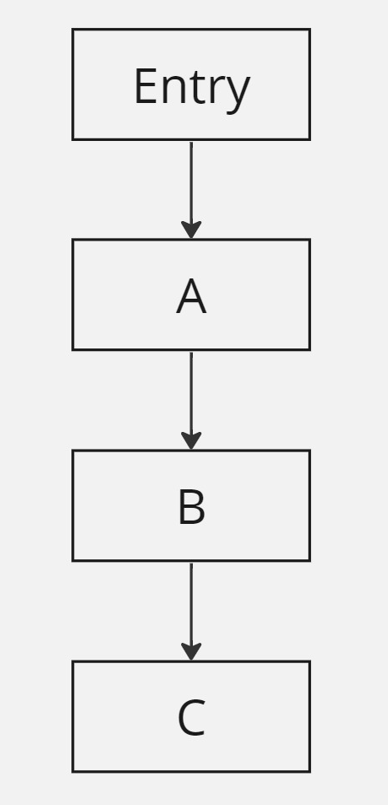
由于上图中除 Entry 外所有节点的 Immediate Dominator 刚好是该节点的父节点，因此上图的 Dominator Tree 的图刚好和上图本身是一样的，故我就不再重复给一遍上图的 Dominator Tree 的图了，下面我们在说到 Dominator Tree 的时候，读者需要注意到这点（同时也注意，大部分时候一个 Flow Graph 的 Dominator Tree 和 Flow Graph 本身是不一样的，避免乱掉）。

容易得到：

1. \( \mathop{doms}(\text{Entry}) = \{ \text{Entry} \} \)
2. \( \mathop{doms}(A) = \{ A, \text{Entry} \} \)
3. \( \mathop{doms}(B) = \{ B, A, \text{Entry} \} \)
4. \( \mathop{doms}( C) = \{ C, B, A, \text{Entry} \} \)

可以看到，如果选择记录一个节点的 \( \mathop{doms} \) 信息的话，则各节点的 \( \mathop{doms} \) 集合会有很多重复的信息，比如上面各 \( \mathop{doms} \) 集合就都有 \(\text{Entry} \) ，这样比较浪费空间，如果选择仅记录节点的 \( \mathop{idom} \) 信息，则结果如下：

1. \( \mathop{idom}(A) = \{ \text{Entry} \} \)
2. \( \mathop{idom}(B) = \{ A \} \)
3. \( \mathop{idom}( C) = \{ B \} \)

可以看到，信息的重复度减少了，此时如果要还原 \( \mathop{doms} \) 集合的话，则像前面说的，顺着 Dominator Tree 往上走，记录经过的所有节点即可。

我们现在要证明上述还原 \( \mathop{doms} \) 集合方法的正确性，首先给上面“顺着 Dominator Tree 往上走，记录经过的所有节点”这个动作记号化：

记号 1.2 （节点的所有祖先）：

给定树 \( G(V, E, R) \) ，这里 \( V \) 为节点集， \( E \) 为边集， \( R \) 为根节点 ，给定节点 \( A \in V \)，则记 \( A \) 所有祖先节点组成的集合为 \( \mathop{ANCES}_G(A) \) ，特别的， \( A \) 本身也是自己的祖先，即 \( A \in \mathop{ANCES}_G(A) \) 。

定义记号完毕。

我们现在证明上述还原 \( \mathop{doms} \) 集合方法的正确性：

定理 1.12 （ \( \mathop{doms} \) 集合可通过 Immediate Dominator 还原）：

给定 Flow Graph \( G(V, E, \text{Entry}) \) ，针对任意\( A \in V \) ， \( A \) 在 \( G \) 的 Dominator Tree 中的所有祖先节点组成的集合为 \( \mathop{ANCES}_{\mathop{DT}(G)}(A) \) ，我们断言 \( \mathop{ANCES}_{\mathop{DT}(G)}(A) = \mathop{doms}(A) \) 。

证明：

我们得证明 \( \mathop{ANCES}_{\mathop{DT}(G)}(A) \subseteq \mathop{doms}(A) \) 以及 \( \mathop{doms}(A) \subseteq \mathop{ANCES}_{\mathop{DT}(G)}(A) \) 。

先证明 \( \mathop{ANCES}_{\mathop{DT}(G)}(A) \subseteq \mathop{doms}(A) \) ：

\( \forall B \in \mathop{ANCES}_{\mathop{DT}(G)}(A) \) ，由于 \( B \) 是 \( A \) 在 \( \mathop{DT}(G) \) 中的祖先节点之一，因此存在由 \( \mathop{DT}(G) \) 的树边组成的路径 \( p = [x_1, x_2, \dots, x_n], x_1 = B, x_n = A \) ，如果 \( n = 1 \) ，则 \( B = A \) ，直接可得 \( B \in \mathop{doms}(A) \)，如果 \( n > 1 \) ，则根据 \( \mathop{DT}(G) \) 边的定义，可得 \( \forall 1 \leq i \leq n - 1, x_i \mathop{idom} x_{i + 1} \) ，进而可得 \( \forall 1 \leq i \leq n - 1, x_i \mathop{dom} x_{i + 1} \) ，再由传递性，可得 \( (x_1 = B) \mathop{dom} (x_n = A) \) ，这意味着 \( B \in \mathop{doms}(A) \) 。

最后证明 \( \mathop{doms}(A) \subseteq \mathop{ANCES}_{\mathop{DT}(G)}(A) \) ：

记 \( \mathop{doms}(A) \) 的元素数量为 \( m \) ，对 \( m \) 进行数学归纳：

当 \( m = 1 \) 时， \( \mathop{doms}(A) \) 只有一个元素，由 定理 1.10 以及 定理 1.2 ，可得 \( A = \text{Entry}, \mathop{doms}(A) = \{ \text{Entry} \} \) ，此时 \( \forall B \in \mathop{doms}(A) \) ，有 \( B = \text{Entry} \) ，这意味着 \( B \) 是 \( \mathop{DT}(G) \) 的根节点，进而 \( B \) 是 \( A \) 的祖先节点，可得 \( B \in \mathop{ANCES}_{\mathop{DT}(G)}(A) \) ，至此有 \( \mathop{doms}(A) \subseteq \mathop{ANCES}_{\mathop{DT}(G)}(A) \) ，可得 \( m = 1 \) 时命题成立。

归纳假设当 \( m = k \) 时命题成立，当 \( m = k + 1 \) 时， \( A \) 的 Dominator 的数量超过 1 了， 我们知道它不是 Entry ，于是由 定理 1.10 ，可得 \( A \) 有 Immediate Dominator \( \text{IDOM}(A) \) ，令 \( I = \text{IDOM}(A) \) ，我们证明 \( \mathop{doms}(I) \) 的节点数量为 \( k \) , 为此，我们仅需要证明 \( \mathop{doms}(I) = \mathop{doms}(A) \setminus \{ A \} \) 即可，因为后者的节点数量明显为 \( (k + 1) - 1 = k \) ，先证明 \( \mathop{doms}(I) \subseteq \mathop{doms}(A) \setminus \{ A \} \) ， \( \forall J \in \mathop{doms}(I) \) ，有 \( J \mathop{dom} I \mathop{sdom} A \) ，进而有 \( J \mathop{sdom} A \) ，可得 \( J \in \mathop{doms}(A) \setminus \{ A \} \) ，再证明 \( \mathop{doms}(A) \setminus \{ A \} \subseteq \mathop{doms}(I) \) ， \( \forall B \in \mathop{doms}(A) \setminus \{ A \} \) ，有 \( B \mathop{sdom} A \) ，由 Immediate Dominator 的定义，可得 \( B \mathop{dom} (I = \text{IDOM}(A)) \) ，进而可得 \( B \in \mathop{doms}(I) \) ，综上，有 \( \mathop{doms}(I) = \mathop{doms}(A) \setminus \{ A \} \) ，于是可知 \( \mathop{doms}(I) \) 的节点数量为 \( k \) ，根据归纳假设，可得 \( \mathop{doms}(I) \subseteq \mathop{ANCES}_{\mathop{DT}(G)}(I) \) (1) ，又 \( \mathop{doms}(A) = \mathop{doms}(I) \cup \{ A \}, \mathop{ANCES}_{\mathop{DT}(G)}(A) = \mathop{ANCES}_{\mathop{DT}(G)}(I) \cup \{ A \} \) ，这意味着在 (1) 处关系式两边并上 \( \cup \{ A \} \) ，可得 \( \mathop{doms}(A) \subseteq \mathop{ANCES}_{\mathop{DT}(G)}(A) \) ，至此有 \( m = k + 1 \) 时命题成立。

至此，归纳完毕，命题成立，结论是 \( \mathop{doms}(A) \subseteq \mathop{ANCES}_{\mathop{DT}(G)}(A) \) 。

综上，有 \( \mathop{ANCES}_{\mathop{DT}(G)}(A) = \mathop{doms}(A) \) 。

证毕。

结语

至此，Dominator 及其相关概念的定义以及性质的证明就讲完了。

以后可能会补充：图的遍历算法、生成树、图边的分类（树边、前向边、后向边、交叉边）、以及各个东西相关性质的讲解和证明，包括为什么交叉边不可能往右拐（这里的右指的是，读者面向屏幕看着图，图的各个生成树的根画在上方，树边方向往下，然后树的孩子按被深度遍历到的先后顺序从左到右画，先遍历到的孩子画在后遍历到的孩子的左边，此时你屏幕的右边就是我说的右边），这些东西对理解 Tarjan 的 Dominator 算法来说是必要的（ Tarjan 算法 是目前最常用且最快的 Dominator 算法，其算法复杂度不是线性的，虽然现在已经有线性复杂度的 Dominator 算法，但是由于其实现复杂，导致其时间复杂度中 \( O(a(m + n) + c) \) 中的系数 \( a \) 以及常数项 \( c \) 比较大，针对实际实践中遇到的图，都会是 Tarjan 算法更快）。

原本是打算至少要写 Purdom 算法、 Iterative 算法、 Cooper 算法 、 Tarjan 算法这多个 Dominator 算法的描述和证明的，但是在刚要证明 Purdom 算法中用到的非常简单的 Reachable 算法时，发现如果按有副作用的写法去写（ visited + 递归），即使这么简单的算法，证明都得写得很长，如果按没副作用的写法去写，证明就很简单了，但是我们在实际实践中为了性能并不会这样写，这点是让我不满意的，于是目前我放弃了写这几个算法的证明，看以后有没有动力补上吧。

Dominator 算法相关的参考文献

最后，附上多个 Dominator 算法相关的参考文献：

• Building an optimizing compiler 1st ：讲解了图的遍历以及边的分类算法，讲解了 Purdom Dominator 算法，简要提及了 Tarjan Dominator 算法。
• Compilers: Principles, Techniques, and Tools 2nd ：讲解了数据流分析框架及其形式化，同时给了相关性质的证明，讲解了 Iterative Dominator 算法， Iterative Dominator 算法的正确性可以通过数据流分析框架一下子证出来，也可以直接证明，不需要用到数据流分析框架的理论。一个题外话：数据流分析框架论文的起始是 A Unified Approach to Global Program Optimization （该理论需要 Lattice 理论的知识，推荐看 Introduction to Lattices and Order 2nd ），其给了算法正确性的证明，论文的大方向是没问题的，但是证明有几个地方有问题，比如 Lemma 2 的证明假设了 \( X \) 是有限集（对 \( X \) 的基数进行了数学归纳），但是后面证明 Theorem 2 用 Lemma 2 的时候，\( X \) 的元素为路径且路径的数量可能是无限的，也就是 \( X \) 可能是无限集（虽然是可数集），一种修正办法是要求 meet-semilattice 满足 descending chain condition ，这样针对 \( X \) 为可数无限集的情况下的 \( \bigwedge_{x \in X} x \) ，给每个 \( x \) 一个序号（ \( X \)是可数集，所以可以做到 ），就可得 \( \exists m \in \mathbf{N}, \forall n \geq m, \bigwedge_{i = 1}^{n} x_i = \bigwedge_{i = 1}^{m} x_i \) ，进而可以定义 \( \bigwedge_{x \in X} x = \bigwedge_{i = 1}^{m} x_i \) ，此时可数无限集的情况就转换成有限集的情况了，不过整个论文可读性很好，给了很多动机的说明，另外一篇论文 Monotone data flow analysis frameworks-Kam-Ullman 扩展了 A Unified Approach to Global Program Optimization 中的方法，去除了对分配律（ distributivity ）的要求，给出了单调数据流分析框架，仅仅需要 transfer 函数是保序的，而不一定要是 distributive 就能保证解的存在，证明了算法能正确计算出 MFP ，且在满足分配律的情况下， MFP = MOP ，进而算法能正确计算出 MOP ，最后，论文证明了不存在算法能做到针对任意单调数据流分析框架问题正确计算出对应的 MOP 解，即单调数据流分析框架的 MOP 解是 undecidable 的问题（理解该证明需要有形式语言、自动机、可计算性理论的相关知识，推荐看 Introduction to Automata Theory, Languages, and Computation 的第1和第3版）。
• A Simple, Fast Dominance Algorithm ：给出了 Cooper Dominator 算法，针对 Iterative Dominator 算法进行改进，使用 Immediate Dominator 链来隐式表示 Dominator 集合，节省了空间，同时使用了一个更快的交集算法，避免了 Dominator 集合交集一堆重复的操作导致速度慢（如果不是用 bit-vector 实现的话）。
• A Fast Algorithm for Finding Dominators in a Flowgraph ：给出了 Tarjan Dominator 算法，引入了 Semi-Dominator 的概念，证明了 Semi-Dominator 的多个性质，利用 Semi-Dominator 的性质，按 depth-first number 降序的顺序计算出各个节点的 Immediate Dominator ，算法设计非常巧妙，各个地方都巧妙地复用、节省了空间，就跟 Tarjan 计算 Strongly Connected Component 的算法一样，各个步骤之间配合好得就跟魔法一样。
• Applications of Path Compression on Balanced Tree ： A Fast Algorithm for Finding Dominators in a Flowgraph 中给出的 Tarjan Dominator 算法为了节省计算出某个节点到树的根节点（这个树是临时构建的树，会随着计算一直扩展，直到变成图的某个生成树）之间具有最小 Semi-Dominator 的中间节点所花费的时间，会对构建的树的路径进行压缩，同时可选的，可以对树进行平衡，保证树的深度浅，进一步减少花费的时间，这篇论文详细讲了用到的路径压缩和树平衡算法。需要注意的是，这里的树平衡并不是常规意义上的树平衡，具体的，“平衡后”的整个树的深度可能还是很深，这里算法实际上是将整个树分成一个个深度浅的子树，且确保我们要获取某个节点到树的根节点之间具有最小 Semi-Dominator 的中间节点时，只需要考虑某个深度较浅的子树就行，进而整个树的深度深并不要紧，从这个意义上来讲，整个树是“平衡”的，具体细节请读者自行看论文的第 5 章节。
• Finding Dominators Revisited ：给出了线性复杂度的 Dominator 计算算法，这篇论文我还没看。
• Finding Dominators in Practice ：给出了 Semi-NCA Dominator 算法， LLVM 为了在 Flow Graph 改变的时候，不重新计算 Dominator 关系，而是尽量增量更新（ incremental update ） Dominator 的关系信息, 于是从用 Tarjan Dominator 算法改成用 Semi-NCA Dominator 算法，具体看视频： 2017 LLVM Developers’ Meeting: J. Kuderski “Dominator Trees and incremental updates that … ” ，这篇论文我还没看。