Types and Programming Languages习题的参考解答及思考(第23章)
第23章
章节23.4
练习23.4.1
题目:
Using the typing rules in Figure 23-1, convince yourself that the terms above have the types given.

\[ \begin{aligned} &\text{id} = \lambda \text{X. } \lambda \text{x}: \text{X. } \text{x}; \\ \blacktriangleright \text{ } &\text{id} : \forall \text{X. } \text{X} \to \text{X} \end{aligned} \]
\[ \begin{aligned} &\text{id} \text{ } [\text{Nat}]; \\ \blacktriangleright \text{ } &\langle \text{fun} \rangle : \text{Nat} \to \text{Nat} \end{aligned} \]
\[ \begin{aligned} &\text{id} \text{ } [\text{Nat}] \text{ } 0; \\ \blacktriangleright \text{ } &0 : \text{Nat} \end{aligned} \]
\[ \begin{aligned} &\text{double} = \lambda \text{X. } \lambda \text{f}: \text{X} \to \text{X. } \lambda \text{a}: \text{X. } \text{f (f a)}; \\ \blacktriangleright \text{ } &\text{double} : \forall \text{X. } (\text{X} \to \text{X}) \to \text{X} \to \text{X} \end{aligned} \]
\[ \begin{aligned} &\text{doubleNat} = \text{double} \text{ } [\text{Nat}]; \\ \blacktriangleright \text{ } &\text{doubleNat} : (\text{Nat} \to \text{Nat}) \to \text{Nat} \to \text{Nat} \end{aligned} \]
\[ \begin{aligned} &\text{doubleNatArrow} = \text{double} \text{ } [\text{Nat} \to \text{Nat}]; \\ \blacktriangleright \text{ } &\text{doubleNatArrow} : ((\text{Nat} \to \text{Nat}) \to \text{Nat} \to \text{Nat}) \to (\text{Nat} \to \text{Nat}) \to \text{Nat} \to \text{Nat} \end{aligned} \]
\[ \begin{aligned} &\text{double} \text{ } [\text{Nat}] \text{ } (\lambda \text{x}: \text{Nat. } \text{succ(succ(x))}) \text{ } 3; \\ \blacktriangleright \text{ } &7 : \text{Nat} \end{aligned} \]
\[ \begin{aligned} &\text{selfApp} = \lambda \text{x}: \forall \text{X. } \text{X} \to \text{X. } \text{x } [\forall \text{X. } \text{X} \to \text{X}] \text{ } \text{x}; \\ \blacktriangleright \text{ } &\text{selfApp} : (\forall \text{X. } \text{X} \to \text{X}) \to (\forall \text{X. } \text{X} \to \text{X}) \end{aligned} \]
\[ \begin{aligned} &\text{quadruple} = \lambda \text{X. } \text{double } [\text{X} \to \text{X}] \text{ } (\text{double } [\text{X}]); \\ \blacktriangleright \text{ } &\text{quadruple} : \forall \text{X. } (\text{X} \to \text{X}) \to \text{X} \to \text{X} \end{aligned} \]
解答:
简单且冗长,略。
练习23.4.2
题目:
Convince yourself that \( \text{map} \) really has the type shown.


解答:
简单且冗长,略。
练习23.4.3
Using \( \text{map} \) as a model, write a polymorphic list-reversing function:
\( \text{reverse}: \forall \text{X. } \text{List X} \to \text{List X} \).
解答:
reverse尾列表得到列表rl,然后再append首元素到rl即可,由于 \( \text{cons} \) 只能做到prepend元素到列表,故我们需要先定义一个辅助函数实现append元素到列表, append的实现就是简单的递归定义,首先考虑空列表的情况,接着考虑至少有一个元素+尾列表的情况,并递归处理尾列表,具体如下:
\( \begin{aligned} \text{append} = &\text{ }\lambda \text{X. } (\text{fix } (\lambda \text{self}: \text{List X} \to \text{X} \to \text{List X. } \\ &\quad \quad \quad \lambda \text{l}: \text{List X. } \lambda \text{e}: \text{X. } \\ &\quad \quad \quad \quad \text{if isnil } [\text{X}] \text{ l} \\ &\quad \quad \quad \quad \text{then } \text{cons } [\text{X}] \text{ e l} \\ &\quad \quad \quad \quad \text{else } \text{cons } [\text{X}] \text{ } (\text{head } [\text{X}] \text{ l}) \text{ } (\text{self } (\text{tail } [\text{X}] \text{ l}) \text{ e}))) \end{aligned} \)
\( \begin{aligned} \text{reverse} = &\text{ }\lambda \text{X. } (\text{fix } (\lambda \text{self}: \text{List X} \to \text{List X. } \\ &\quad \quad \quad \lambda \text{l}: \text{List X. } \\ &\quad \quad \quad \quad \text{if isnil } [\text{X}] \text{ l} \\ &\quad \quad \quad \quad \text{then } \text{nil } [\text{X}] \\ &\quad \quad \quad \quad \text{else } \text{append } [\text{X}] \text{ } (\text{self } (\text{tail } [\text{X}] \text{ l})) \text{ } (\text{head } [\text{X}] \text{ l}))) \end{aligned} \)
练习23.4.4
题目:
Write a simple polymorphic sorting function
\( \text{sort}: \forall \text{X. } (\text{X} \to \text{X} \to \text{Bool}) \to (\text{List X}) \to \text{List X} \)
where the first argument is a comparison function for elements of type \( \text{X} \).
解答:
merge sort用递归能很自然地表达,这里我们固定把左区间分成单元素列表,即由首元素单独组成的列表,右区间则直接取尾列表, sort完右区间后,再合并单元素列表和已经排序完的尾列表,得到的算法就是insertion sort,如下:
\( \begin{aligned} \text{sort} = &\text{ }\lambda \text{X. } (\text{fix } (\lambda \text{self}: (\text{X} \to \text{X} \to \text{Bool}) \to (\text{List X}) \to \text{List X} \\ &\quad \quad \quad \lambda \text{leq}: \text{X} \to \text{X} \to \text{Bool.} \\ &\quad \quad \quad \lambda \text{l}: \text{List X.} \\ &\quad \quad \quad \quad \text{if isnil } [\text{X}] \text{ l} \text{ then } \text{nil } [\text{X}] \\ &\quad \quad \quad \quad \text{else } \text{mergeHeadAndSortedTail } [\text{X}] \text{ leq } (\text{head } [\text{X}] \text{ l}) \text{ } (\text{self } (\text{tail } [\text{X}] \text{ l})))) \end{aligned} \)
\( \begin{aligned} \text{mergeHeadAndSortedTail} = &\text{ }\lambda \text{X. } (\text{fix } (\lambda \text{self}: \text{X} \to (\text{List X}) \to \text{List X} \\ &\quad \quad \quad \lambda \text{leq}: \text{X} \to \text{X} \to \text{Bool.} \\ &\quad \quad \quad \lambda \text{h}: \text{X.} \\ &\quad \quad \quad \lambda \text{t}: \text{List X.} \\ &\quad \quad \quad \quad \text{if isnil } [\text{X}] \text{ t} \text{ then } \text{cons } [\text{X}] \text{ h } (\text{nil } [\text{X}]) \\ &\quad \quad \quad \quad \text{else if leq h } (\text{head } [\text{X}] \text{ t}) \text{ then } \text{cons } [\text{X}] \text{ h t} \\ &\quad \quad \quad \quad \text{else } \text{cons } [\text{X}] \text{ } (\text{head } [\text{X}] \text{ t}) \text{ } (\text{self leq h } (\text{tail } [\text{X}] \text{ t})))) \end{aligned} \)
练习23.4.5
题目:
Write a term \( \text{and} \) that takes two arguments of type \( \text{CBool} \) and computes their conjunction.
解答:
\( \text{and } = \lambda \text{b1}: \text{Bool. } \lambda \text{b2}: \text{Bool. } \lambda \text{X. } \lambda \text{t}: \text{X. } \lambda \text{f}: \text{X. } \text{b1 } [\text{X}] \text{ } (\text{b2 } [\text{X}] \text{ t f} ) \text{ f} \)
练习23.4.6
题目:
Write a function \( \text{iszro} \) that will return \( \text{tru} \) when applied to the Church numeral \( \text{c0} \) and \( \text{fls} \) otherwise.
解答:
\( \text{iszro} = \lambda \text{n}: \text{CNat. } \text{n } [\text{Bool}] \text{ } (\lambda \text{b}: \text{Bool. } \text{fls}) \text{ tru} \)
练习23.4.7
题目:
Verify that the terms
\( \begin{aligned} &\text{ctimes} = \lambda \text{m}: \text{CNat. } \text{n}: \text{CNat. } \lambda \text{X. } \lambda \text{s}: \text{X} \to \text{X. } \text{n } [\text{X}] \text{ } (\text{m } [\text{X}] \text{ s}) \\ \blacktriangleright \text{ } &\text{ctimes} : \text{CNat} \to \text{CNat} \to \text{CNat} \end{aligned} \)
\( \begin{aligned} &\text{cexp} = \lambda \text{m}: \text{CNat. } \text{n}: \text{CNat. } \lambda \text{X. } \text{n } [\text{X} \to \text{X}] \text{ } (\text{m } [\text{X}]) \\ \blacktriangleright \text{ } &\text{cexp} : \text{CNat} \to \text{CNat} \to \text{CNat} \end{aligned} \)
have the indicated types. Give an informal argument that they implement the arithmetic multiplication and exponentiation operators.
解答:
首先说明为什么\( \text{ctimes}, \text{cexp} \)具有上述的类型,先从\( \text{ctimes} \)开始:
\( \text{s} \)具有类型\( \text{X} \to \text{X} \),而\( \text{CNat} = \forall \text{X. } (\text{X} \to \text{X}) \to \text{X} \to \text{X} \),因此\( \text{m } [\text{X}] \text{ s} \)具有类型\( \text{X} \to \text{X} \),进而\( \text{n } [\text{X}] \text{ } (\text{m } [\text{X}] \text{ s}) \) 具有类型\( \text{X} \to \text{X} \),最终我们得到结论:\( \lambda \text{X. } \lambda \text{s}: \text{X} \to \text{X. } \text{n } [\text{X}] \text{ } (\text{m } [\text{X}] \text{ s}) \)具有类型 \( \forall \text{X. } (\text{X} \to \text{X}) \to \text{X} \to \text{X} \),也就是\( \text{CNat} \),综上,\( \text{ctimes} \)具有类型\( \text{CNat} \to \text{CNat} \to \text{CNat} \)。
接着是\( \text{cexp} \):
\( \text{m } [\text{X}] \)具有类型 \( (\text{X} \to \text{X}) \to \text{X} \to \text{X} \),而\( \text{n } [\text{X} \to \text{X}] \text{ } \)具有类型 \( ((\text{X} \to \text{X}) \to (\text{X} \to \text{X})) \to (\text{X} \to \text{X}) \to (\text{X} \to \text{X}) \),进而\( \text{n } [\text{X} \to \text{X}] \text{ } (\text{m } [\text{X}]) \)具有类型 \( (\text{X} \to \text{X}) \to (\text{X} \to \text{X}) = (\text{X} \to \text{X}) \to \text{X} \to \text{X} \)。最终我们得到结论:\( \lambda \text{X. } \text{n } [\text{X} \to \text{X}] \text{ } (\text{m } [\text{X}]) \)具有类型 \( \forall \text{X. } (\text{X} \to \text{X}) \to \text{X} \to \text{X} \),也就是\( \text{CNat} \),综上,\( \text{ctimes} \)具有类型\( \text{CNat} \to \text{CNat} \to \text{CNat} \)。
最后我们说明下为什么\( \text{ctimes m n} \)可以计算\( \text{m} \times \text{n} \),而\( \text{cexp m n} \)可以计算\( \text{m}^{\text{n}} \),先从\( \text{ctimes} \)开始:
求值\( \text{m } [\text{X}] \text{ s} \),我们会得到一个单参数函数\( \text{f} \),它接收一个起始值\( \text{z} \),并以\( \text{z} \)为起始值迭代调用\( \text{s} \)共\( \text{m} \)次,返回\( \text{m} \)次迭代调用后的结果值,结果值的类型和\( \text{z} \)是一样的,紧接着,我们会求值\( \text{n } [\text{X}] \text{ f} \),也得到一个单参数函数\( \text{g} \),它接收一个起始值\( \text{z} \),并以\( \text{z} \)为起始值迭代调用\( \text{f} \)共\( \text{n} \)次,返回\( \text{n} \)次迭代调用后的结果值,结果值的类型和\( \text{z} \)是一样的。可得,迭代调用\( \text{f} \)共\( \text{n} \)次实际上就相当于迭代调用\( \text{s} \)共\( \text{m} \times \text{n} \)次,也就是\( \text{g} \)的作用是:接收一个起始值\( \text{z} \),并以\( \text{z} \)为起始值迭代调用\( \text{s} \)共\( \text{m} \times \text{n} \)次。最终我们求值得到的结果是\( \lambda \text{X. } \lambda \text{s}: \text{X} \to \text{X. } \text{g} \),不考虑类型参数\( \text{X} \)的话,它接收一个后继函数参数\( \text{s} \),以及接收一个起始值\( \text{z} \)(由\( \text{g} \)接收),然后以\( \text{z} \)为起始值迭代调用\( \text{s} \)共\( \text{m} \times \text{n} \)次并返回,返回值类型和\( \text{z} \)一样。综上,\( \text{ctimes m n} \)能正确计算\( \text{m} \times \text{n} \)。
接着是\( \text{cexp} \):
求值\( \text{m } [\text{X}] \),我们会得到一个双参数函数\( \text{f} \),它接收后继函数\( \text{s} \)和起始值\( \text{z} \),并以\( \text{z} \)为起始值迭代调用\( \text{s} \)共\( \text{m} \)次,返回\( \text{m} \)次迭代调用后的结果值,结果值的类型和\( \text{z} \)是一样的,紧接着,我们会求值\( \text{n } [\text{X} \to \text{X}] \text{ f} \),也得到一个单参数函数\( \text{g} \),它接收一个起始值\( \text{s} \),并以\( \text{s} \)为起始值迭代调用\( \text{f} \)共\( \text{n} \)次,返回\( \text{n} \)次迭代调用后的结果值,结果值的类型和\( \text{s} \)是一样的。以\( \text{s} \)为起始值迭代调用\( \text{f} \)共\( \text{n} \)次的作用不好直接看出来,我们先看一次调用\( \text{f s} \)的效果,这里会返回一个单参数函数\( \text{f}_1 \),它接收一个起始值\( \text{z} \),并以\( \text{z} \)为起始值迭代调用\( \text{s} \)共\( \text{m} \)次,接着看迭代两次调用\( \text{f (f s)} = \text{f } \text{f}_1 \)的效果,返回单参数函数\( \text{f}_2 \),它接收一个起始值\( \text{z} \),并以\( \text{z} \)为起始值迭代调用\( \text{f}_1 \)共\( \text{m} \)次,一次\( \text{f}_1 \)的调用相当于\( \text{m} \)次\( \text{s} \)的迭代调用,进而\( \text{m} \)次\( \text{f}_1 \)的迭代调用相当于\( \text{m} \times \text{m} = \text{m}^2 \)次\( \text{s} \)的迭代调用,以此类推,可得,以\( \text{s} \)为起始值迭代调用\( \text{f} \)共\( \text{n} \)次,会得到一个单参数函数\( \text{f}_n \),它接收一个起始值\( \text{z} \),并以\( \text{z} \)为起始值迭代调用\( \text{s} \)共\( \text{m}^\text{n} \)次,综上,最终求值结果是单参数函数\( \text{g} \),它接收一个起始值\( \text{s} \),并以\( \text{s} \)为起始值迭代调用\( \text{f} \)共\( \text{n} \)次,并返回另外一个单参数函数\( \text{f}_n \),它接收一个起始值\( \text{z} \),并以\( \text{z} \)为起始值迭代调用\( \text{s} \)共\( \text{m}^\text{n} \)次,一个单参数函数返回另外一个单参数函数,实际上就是双参数函数,接收后继函数\( \text{s} \)以及起始值\( \text{z} \),并以\( \text{z} \)为起始值迭代调用\( \text{s} \)共\( \text{m}^\text{n} \)次,可得,\( \text{cexp m n} \)能正确计算\( \text{m}^{\text{n}} \)。
练习23.4.8
题目:
Show that the type
\( \text{PairNat} = \forall \text{X. } (\text{CNat} \to \text{CNat} \to \text{X}) \to \text{X} \);
can be used to represent pairs of numbers, by writing functions
\( \text{pairNat} : \text{CNat} \to \text{CNat} \to \text{PairNat} \);
\( \text{fstNat} : \text{PairNat} \to \text{CNat} \);
\( \text{sndNat} : \text{PairNat} \to \text{CNat} \);
for constructing elements of this type from pairs of numbers and for accessing their first and second components.
解答:
\( \text{pairNat} = \lambda \text{n}_1: \text{CNat. } \lambda \text{n}_2: \text{CNat. } \lambda \text{X. } \lambda \text{f}: \text{CNat} \to \text{CNat} \to \text{X. } \text{f } \text{n}_1 \text{ } \text{n}_2 \)
\( \text{fstNat} = \lambda \text{p}: \text{PairNat. } \text{p } [\text{CNat}] \text{ } (\lambda \text{n}_1: \text{CNat. } \lambda \text{n}_2: \text{CNat. } \text{n}_1) \)
\( \text{sndNat} = \lambda \text{p}: \text{PairNat. } \text{p } [\text{CNat}] \text{ } (\lambda \text{n}_1: \text{CNat. } \lambda \text{n}_2: \text{CNat. } \text{n}_2) \)
练习23.4.9
题目:
Use the functions defined in Exercise 23.4.8 to write a function \( \text{prd} \) that computes the predecessor of a Church numeral (returning \( 0 \) if its input is \( 0 \)). Hint: the key idea is developed in the example in \( \S 5.2 \). Define a function \( \text{f}: \text{PairNat} \to \text{PairNat} \) that maps the pair \( (i, j) \) into \( (i + 1, i) \)—that is, it throws away the second component of its argument, copies the first component to the second, and increments the first. Then \( n \) applications of \( f \) to the starting pair \( (0, 0) \) yields the pair \( (n, n - 1) \), from which we extract the predecessor of \( n \) by projecting the second component.
解答:
\( \text{pairSucc} = \lambda \text{p}: \text{PairNat. } \lambda \text{n}: \text{CNat. } \text{pairNat } (\text{cplus } \text{c}_1 \text{ } \text{fstNat p}) \text{ } (\text{fstNat p}) \)
\( \text{prd} = \lambda \text{n}: \text{CNat. } \text{sndNat } (\text{n } [\text{PairNat}] \text{ pairSucc } (\text{pairNat } \text{c}_0 \text{ } \text{c}_0)) \)
练习23.4.10
题目:
There is another way of computing the predecessor function on Church numerals. Let \( \text{k} \) stand for the untyped lambda-term \( \lambda \text{x. } \lambda \text{y. } \text{x} \) and \( \text{i} \) for \( \lambda \text{x. } \text{x} \). The untyped lambda-term
\( \text{vpred} = \lambda \text{n. } \lambda \text{s. } \lambda \text{z. } \text{n } (\lambda \text{p. } \lambda \text{q. } \text{q } (\text{p s})) \text{ } (\text{k z}) \text{ i} \)
(from Barendregt, 1992, who attributes it to J. Velmans) computes the predecessor of an untyped Church numeral. Show that this term can be typed in System F by adding type abstractions and applications as necessary and annotating the bound variables in the untyped term with appropriate types. For extra credit, explain why it works!
解答:
我们先讲下为什么\( \text{vpred} \)能正确计算前继,后面再讲怎么赋予类型的问题:
从\( \text{vpred} \)的参数命名就可以猜到, \( \text{n} \)应该是个\( \text{CNat} \),然后\( \text{s} \)应该是个后继函数,具体类型不确定, \( \text{z} \)应该是个起始值,具体类型不确定,然后\( \text{p}, \text{q} \)原本猜是某种类型的\( \text{Pair} \),后面发现不是,现在我们暂定不假定\( \text{p}, \text{q} \)有什么类型和作用,等下再考虑。
先看\( \text{k} \),它接收两个参数\( \text{x}, \text{y} \),并且无视第二个参数\( \text{y} \),无脑返回第一个参数\( \text{x} \),也就是它的作用是记忆住第一个参数,然后随便给个参数,它就能返回它记忆的那个参数。
接着看\( \text{k z} \),效果就是记忆住参数\( \text{z} \),然后返回一个单参数函数\( \text{r} \),你随便给\( \text{r} \)一个参数,它都会返回它记忆的参数\( \text{z} \)。
接着看\( \text{n } (\lambda \text{p. } \lambda \text{q. } \text{q } (\text{p s})) \text{ } (\text{k z}) \),效果是以\( \text{k z} \)为起始值,迭代调用\( \lambda \text{p. } \lambda \text{q. } \text{q } (\text{p s}) \) 共\( \text{n} \)次,作用不好看出来,所以我们逐步看每次迭代调用的效果:
第一次迭代调用为\( (\lambda \text{p. } \lambda \text{q. } \text{q } (\text{p s})) \text{ } (\text{k z}) \),将\( \text{k z} \)作为参数\( \text{p} \)代入函数体,我们会得到\( \lambda \text{q. } \text{q } ((\text{k z}) \text{ s}) \),这里\( \text{k} \)记忆住了它的第一个参数\( \text{z} \),然后我们又随便给了它个参数\( \text{s} \),于是它返回了它记忆的参数\( \text{z} \),因此\( (\text{k z}) \text{ s} \)会求值得到\( \text{z} \),进而可得第一次迭代调用得到的是\( \lambda \text{q. } \text{q } \text{z} \),我们记\( \text{f}_1 = \lambda \text{q. } \text{q } \text{z} \)。
接着考虑第二次迭代调用,为\( (\lambda \text{p. } \lambda \text{q. } \text{q } (\text{p s})) \text{ } \text{f}_1 \) 将\( \text{f}_1 \)作为参数\( \text{p} \)代入函数体,我们会得到\( \lambda \text{q. } \text{q } (\text{f}_1 \text{ s}) \),这里\( \text{f}_1 \text{ s} = (\lambda \text{q. } \text{q } \text{z}) \text{ s} \)会求值得到\( \text{s z} \) 进而可得第二次迭代调用得到的是\( \lambda \text{q. } \text{q } (\text{s z}) \),我们记\( \text{f}_2 = \lambda \text{q. } \text{q } (\text{s z}) \)。
类似上面,容易得到\( \text{f}_3 = \lambda \text{q. } \text{q } (\text{s (s z)}) \),以此类推,可得第\( \text{n} \)次迭代调用后的结果值为\( \text{f}_n = \lambda \text{q. } \text{q } (\text{s}^{\text{n} - 1} \text{ z}) \),这里\( \text{s}^{\text{n} - 1} \text{ z} \)为以\( \text{z} \)为初始值,迭代调用\( \text{s} \)共\( \text{n - 1} \)次的缩写。
综上,求值\( \text{n } (\lambda \text{p. } \lambda \text{q. } \text{q } (\text{p s})) \text{ } (\text{k z}) \) 会得到\( \text{f}_n = \lambda \text{q. } \text{q } (\text{s}^{\text{n} - 1} \text{ z}) \)。此时函数体会进一步求值\( \text{f}_n \text{ i} \),得到的是\( \text{s}^{\text{n} - 1} \text{ z} \),最终可得\( \text{vpred n} \)求值得到的是\( \lambda \text{s. } \lambda \text{z. } \text{s}^{\text{n} - 1} \text{ z} \),也就是\( \text{n} \)的前继了。
综上,\( \text{vpred} \)能正确计算前继。
现在,我们讲如何给这些项赋予类型,由于题目没有限制我们怎么赋予项类型,故我们按最自然的想法/愿望来考虑,问自己,这个项的作用是什么,它应该要有什么类型:
首先,参数\( \text{n} \)的类型应该是\( \text{CNat} \),然后由于\( \text{CNat} = \forall \text{X. } (\text{X} \to \text{X}) \to \text{X} \to \text{X} \),可得\( \text{s} \)的类型应该是\( \text{X} \to \text{X} \),而\( \text{z} \)的类型应该是\( \text{X} \), \( \text{s} \)中的类型变量\( \text{X} \)和\( \text{z} \)的类型变量\( \text{X} \) 应该要是同一类型,因此我们不能分别为\( \text{s}, \text{z} \)引入两个独立的类型变量,而应该在它们外部引入一个类型变量\( \text{X} \)供\( \text{s}, \text{z} \)共同使用,于是目前可得\( \text{vpred} \)大概长如下这样:
\( \text{vpred} = \lambda \text{n}: \text{CNat. } \lambda \text{X. } \lambda \text{s}: \text{X} \to \text{X. } \lambda \text{z}: \text{X. } \text{n } (\lambda \text{p. } \lambda \text{q. } \text{q } (\text{p s})) \text{ } (\text{k z}) \text{ i} \)
这里需要注意下,\( \text{CNat} \)中的类型变量\( \text{X} \)是独立类型变量,和\( \text{vpred} \)引入的类型变量\( \text{X} \)不一定要实例化成同类型,为了避免歧义,我们改下\( \text{CNat} \)的类型变量名: \( \text{CNat} = \forall \text{Y. } (\text{Y} \to \text{Y}) \to \text{Y} \to \text{Y} \)
接着,我们看\( \text{n } (\lambda \text{p. } \lambda \text{q. } \text{q } (\text{p s})) \text{ } (\text{k z}) \),由\( \text{CNat} \)的定义,可得\( \lambda \text{p. } \lambda \text{q. } \text{q } (\text{p s}) \)的类型应该是\( \text{Y} \to \text{Y} \),而\( \text{k z} \)的类型应该是\( \text{Y} \),进而可得\( \text{t}_1 = \text{n } (\lambda \text{p. } \lambda \text{q. } \text{q } (\text{p s})) \text{ } (\text{k z}) \)的类型应该是\( \text{Y} \),函数体会求值\( \text{t}_1 \text{ i} \),而\( \text{t}_1 \)的类型是\( \text{Y} \),这意味着\( \text{Y} \)应该是函数类型才对,我们写作\( \text{Y} = \text{Z} \to \text{A} \),于是可得\( \text{i} \)的类型应该是\( \text{Z} \),而\( \text{i} \)是identity函数,它应该要能接收任意类型作为参数,可得\( \text{i} = \lambda \text{B. } \lambda \text{x}: \text{B. } \text{x} \),于是有\( \text{Z} = \text{B} \to \text{B} \) (严格来讲应该是\( \text{Z} = \forall \text{B. } \text{B} \to \text{B} \),但是我们之后会给\( \text{i} \)传递类型参数, \( \text{B} \)到时候会变成该传入的类型参数,故这里简写下问题不大)。
接着考虑\( \lambda \text{p. } \lambda \text{q. } \text{q } (\text{p s}) \),我们知道第一次迭代调用的时候,\( \text{p} \)会接收\( \text{k z} \)作为参数,而\( \text{k z} \)的类型为\( \text{Y} \),因此\( \text{p} \)的类型应该是\( \text{Y} \),我们还知道,最后一次函数体会求值\( \text{f}_n \text{ i} = (\lambda \text{q. } \text{q } (\text{s}^{\text{n} - 1} \text{ z})) \text{ i} \),可得\( \text{q} \)会接收\( \text{i} \)作为参数,这意味着\( \text{q} \)的类型应该和\( \text{i} \)一样是\( \text{Z} \)。
再考虑\( \text{k} = \lambda \text{x. } \lambda \text{y. } \text{x} \),由\( \text{k z} \)以及\( \text{z} \)的类型为\( \text{X} \)可得, \( \text{k} \)的类型应该是\( \text{X} \to \text{C} \to \text{X} \), \( \text{x} \)的类型应该是\( \text{X} \),\( \text{y} \)的类型是个未知类型\( \text{C} \),这里\( \text{C} \)类型从哪里来不太清楚,得看哪里传第二个参数\( \text{y} \),我们知道在第一次迭代调用的时候,会求值\( (\text{k z}) \text{ } \text{s} \),这里\( \text{s} \)就是\( \text{k} \)的第二个参数,可得\( \text{C} = \text{X} \to \text{X} \),这意味着\( \text{k} \)的类型应该是\( \text{X} \to (\text{X} \to \text{X}) \to \text{X} \),可得加上类型标注的\( \text{k} = \lambda \text{x}: \text{X. } \lambda \text{y}: \text{X} \to \text{X. } \text{x} \)。
在前面,我们得到了\( \text{k z} \)的类型为\( \text{Y} \),现在我们知道了\( \text{Y} \)更具体的类型:\( \text{Y} = (\text{X} \to \text{X}) \to \text{X} \)。
前面我们还得到了\( \text{Y} = \text{Z} \to \text{A} = (\text{B} \to \text{B}) \to \text{A} \),加上我们刚得到的\( \text{Y} = (\text{X} \to \text{X}) \to \text{X} \),可得\( \text{A} = \text{B} = \text{X} \),进而可得\( \text{Z} = \text{X} \to \text{X} \)。
还差最后两个问题,\( \text{i} \)接收一个类型参数\( \text{B} \),应该传什么类型参数?同理,\( \text{n} \)应该传什么类型参数。先考虑\( \text{i} \),我知道最后函数体会求值\( \text{f}_n \text{ i} = (\lambda \text{q. } \text{q } (\text{s}^{\text{n} - 1} \text{ z})) \text{ i} \),这里\( \text{i} \)是作为参数\( \text{q} \)传入的,而\( \text{q} \)的类型为\( \text{X} \to \text{X} \),可得应该传入\( \text{X} \)作为类型参数。接着考虑\( \text{n} \),\( \text{n} \)的类型为 \( \text{CNat} = \forall \text{Y. } (\text{Y} \to \text{Y}) \to \text{Y} \to \text{Y} \),加上\( \text{n} \)的第二个参数\( \text{k z} \)的类型为\( (\text{X} \to \text{X}) \to \text{X} \),可得应该传入\( (\text{X} \to \text{X}) \to \text{X} \)作为类型参数。
至此可得\( \text{vpred}, \text{k}, \text{i} \)在System F中的定义如下:
\( \begin{aligned} \text{vpred} = &\text{ }\lambda \text{n}: \text{CNat. } \lambda \text{X. } \lambda \text{s}: \text{X} \to \text{X. } \lambda \text{z}: \text{X. } \\ &\quad \text{n } [(\text{X} \to \text{X}) \to \text{X}] \text{ } (\lambda \text{p}: (\text{X} \to \text{X}) \to \text{X. } \lambda \text{q}: \text{X} \to \text{X. } \text{q } (\text{p s})) \text{ } (\text{k z}) \text{ } \text{i } [\text{X}] \end{aligned} \)
\( \text{k} = \lambda \text{x}: \text{X. } \lambda \text{y}: \text{X} \to \text{X. } \text{x} \)
\( \text{i} = \lambda \text{A. } \lambda \text{x}: \text{A. } \text{x} \)
容易验证上述\( \text{vpred} \)在System F下是类型良好的(具体的,验证各个参数和值的类型是否一致,以及多次迭代调用的时候,前一次迭代调用得到的值的类型是否和参数类型一致,等等)。
还容易发现一个问题,\( \text{i} \)的类型参数固定为\( \text{X} \),这意味着我们可以直接用外部的类型参数\( \text{X} \),而不需要\( \text{i} \)自己引入独立的类型参数。简化后如下:
\( \begin{aligned} \text{vpred} = &\text{ }\lambda \text{n}: \text{CNat. } \lambda \text{X. } \lambda \text{s}: \text{X} \to \text{X. } \lambda \text{z}: \text{X. } \\ &\quad \text{n } [(\text{X} \to \text{X}) \to \text{X}] \text{ } (\lambda \text{p}: (\text{X} \to \text{X}) \to \text{X. } \lambda \text{q}: \text{X} \to \text{X. } \text{q } (\text{p s})) \text{ } (\text{k z}) \text{ } \text{i } \end{aligned} \)
\( \text{k} = \lambda \text{x}: \text{X. } \lambda \text{y}: \text{X} \to \text{X. } \text{x} \)
\( \text{i} = \lambda \text{x}: \text{X. } \text{x} \)
练习23.4.11
题目:
Strictly speaking, the examples in this subsection have not been expressed in pure System F, since we used the \( \text{fix} \) operator to construct a value to be “returned” when \( \text{head} \) is applied to an empty list. Write an alternative version of \( \text{head} \) that takes an extra parameter to be returned (instead of diverging) when the list is empty.
解答:
\( \text{head} = \lambda \text{X. } \lambda \text{l}: \text{List X. } \lambda \text{d}: \text{X. } \text{l } [\text{X}] \text{ } (\lambda \text{h}: \text{X. } \lambda \text{t}: \text{X. } \text{h}) \text{ d} \)
练习23.4.12
题目:
In pure System F (without \( \text{fix} \)), write a function \( \text{insert} \) of type
\( \forall \text{X. } (\text{X} \to \text{X} \to \text{Bool}) \to \text{List X} \to \text{X} \to \text{List X} \)
that takes a comparison function, a sorted list, and a new element, and inserts the element into the list at the appropriate point (i.e., after all the elements smaller than it). Next, use \( \text{insert} \) to build a sorting function for lists in pure System F.
解答:
为了将一个元素\( \text{e} \)插入到一个已经排序的列表\( \text{l} \)中,我们选择重新构建一遍列表\( \text{l} \),从右到左(从尾部到首部)逐步按顺序\( \text{cons} \)上\( \text{l} \)中的元素,并在合适的位置把\( \text{e} \)插入进去,确保最终得到的新列表是已排序的。
如果我们限制列表中所有元素都是不同的话(这包括\( \text{l} \)中已有的元素以及刚要插入的元素\( \text{e} \),它们之间都要是不同的),则可以得到一个很简单的\( \text{insert} \)实现,具体的:给列表\( \text{l} \)一个特殊的\( \text{cons} \)函数, \( \text{cons} \)函数可以拿到两个参数\( \text{h}, \text{t} \),这里\( \text{h} \)我们称为当前首元素,\( \text{t} \)我们称为当前尾列表(注意,当前尾列表是已排序的),我们对比当前首元素\( \text{h} \)和要插入的元素\( \text{e} \),如果\( \text{e} < \text{h} \),说明现在还不适合插入, \( \text{e} \)应该插入在列表的更前面,如果\( \text{e} > \text{h} \),则说明可以插入了,自己用不变式(有限数学归纳法)或者简单举个例子试试,很容易验证在限制所有元素不同的条件下,该插入算法是正确的,算法如下:
\( \begin{aligned} \text{insert} = &\text{ } \lambda \text{X. } \lambda \text{leq}: \text{X} \to \text{X} \to \text{Bool. } \lambda \text{l}: \text{List X. } \lambda \text{e}: \text{X. } \\ &\quad \quad \text{l } [\text{List X}] \\ &\quad \quad (\lambda \text{h}: \text{X. } \text{t}: \text{List X. } \\ &\quad \quad \quad \text{if leq e h then cons } [\text{X}] \text{ h t} \\ &\quad \quad \quad \text{else cons } [\text{X}] \text{ h } (\text{cons } [\text{X}] \text{ e t})) \\ &\quad \quad \text{z} \end{aligned} \)
但如果有重复元素的话,则上述算法会产生重复插入\( \text{e} \)的情况,为了避免检测重复,我们可以同时构建两个列表,两个列表中构建的过程中,和上面一样,都是保持排好序的状态,其中一个列表,永远不包含要插入的元素\( \text{e} \),另外一个列表,永远都包含要插入的元素\( \text{e} \),我们称前一个列表为\( \text{listWithOutE} \),后一个列表为\( \text{listWithE} \)。
初始的时候,\( \text{listWithOutE} \)为空列表, \( \text{listWithE} \)则是单元素列表,仅包含一个元素\( \text{e} \)。
考虑比较要插入的元素\( \text{e} \)和当前首元素\( \text{h} \)的时候:
如果\( \text{e} \leq \text{h} \),则\( \text{e}, \text{h} \)都可以插入到\( \text{listWithOutE} \)头部,其中,\( \text{e} \)在\( \text{h} \)前面,即结果列表是\( \text{cons e (cons h listWithOutE)} \),该插入不会破坏已排序的状态,插入后得到新列表仍然是已排序的,且不会有重复插入问题,因为我们知道\( \text{listWithOutE} \)不包含元素\( \text{e} \),我们记\( \text{listWithE}_2 = \text{cons e (cons h listWithOutE)} \),注意,命名上这里不叫\( \text{listWithOutE}_2 \),因为我们该列表有包含\( \text{e} \)。至此,我们得到了新的包含\( \text{e} \)的列表\( \text{listWithOutE}_2 \),还得想办法得到新的不包含\( \text{e} \)的列表,直接把\( \text{h} \)插入到\( \text{listWithOutE} \)头部就行了,得到\( \text{listWithoutE}_2 = \text{cons h listWithOutE} \) (注意,\( \text{e} \leq \text{h} \)的情况下,我们直接会无视掉\( \text{listWithE} \),我们不需要它了,它的作用被\( \text{listWithOutE}_2 \)取代了)。
如果\( \text{h} < \text{e} \),则\( \text{h} \)可以插入到\( \text{listWithE} \)头部,得到\( \text{listWithE}_2 = \text{cons h listWithE} \),由于\( \text{listWithE} \)中已经包含\( \text{e} \)了,因此\( \text{listWithE}_2 \)不需要再插入\( \text{e} \)了,至此,我们得到了新的包含\( \text{e} \)的列表\( \text{listWithOutE}_2 \),还得想办法得到新的不包含\( \text{e} \)的列表,同上,还是直接把\( \text{h} \)插入到\( \text{listWithOutE} \)头部就行了,得到\( \text{listWithoutE}_2 = \text{cons h listWithOutE} \)。
容易看出上面两种情况,均没有重复插入元素\( \text{e} \)的问题。
按上述两种情况不断插入,直到所有元素插入完,我们会得到两个最终列表 \( \text{listWithOutE}_k, \text{listWithE}_k \),这里\( \text{listWithE}_k \)包含了原列表\( \text{l} \)所有元素的同时,还包含了\( \text{e} \),而且还是已排序状态,同时没有重复插入的问题,这就是我们要的最终列表。
我们通过书上刚定义的\( \text{Pair X Y} \)类型来同时维护两个列表,具体的, 我们使用\( \text{Pair (List X) (List X)} \),完整算法如下:
\( \begin{aligned} \text{insert} = &\text{ } \lambda \text{X. } \lambda \text{leq}: \text{X} \to \text{X} \to \text{Bool. } \lambda \text{l}: \text{List X. } \lambda \text{e}: \text{X. } \\ &\quad \quad \text{l } [\text{Pair (List X) (List X)}] \\ &\quad \quad (\lambda \text{h}: \text{X. } \text{p}: \text{Pair (List X) (List X). } \\ &\quad \quad \quad \text{if leq e h then } \\ &\quad \quad \quad \quad \text{pair } [\text{List X}] \text{ } [\text{List X}] \\ &\quad \quad \quad \quad \quad (\text{cons } [\text{X}] \text{ h } (\text{fst } [\text{List X}] \text{ } [\text{List X}] \text{ } \text{p})) \\ &\quad \quad \quad \quad \quad (\text{cons } [\text{X}] \text{ e } (\text{cons } [\text{X}] \text{ h } (\text{fst } [\text{List X}] \text{ } [\text{List X}] \text{ } \text{p}))) \\ &\quad \quad \quad \text{else } \\ &\quad \quad \quad \quad \text{pair } [\text{List X}] \text{ } [\text{List X}] \\ &\quad \quad \quad \quad \quad (\text{cons } [\text{X}] \text{ h } (\text{fst } [\text{List X}] \text{ } [\text{List X}] \text{ } \text{p})) \\ &\quad \quad \quad \quad \quad (\text{cons } [\text{X}] \text{ h } (\text{snd } [\text{List X}] \text{ } [\text{List X}] \text{ } \text{p})) \\ &\quad \quad (\text{pair } [\text{List X}] \text{ } [\text{List X}] \text{ } (\text{nil} [\text{X}]) \text{ } (\text{cons } [\text{X}] \text{ e } (\text{nil } [\text{X}]))) \end{aligned} \)
现在我们可以定义排序函数了,实现在思路上和练习23.4.4是类似的,只不过练习23.4.4那边我们用的\( \text{fix} \),这里利用了列表的\( \text{cons} \)函数,如下:
\( \begin{aligned} \text{sort} = &\text{ }\lambda \text{X. } \lambda \text{leq}: \text{X} \to \text{X} \to \text{Bool. } \lambda \text{l}: \text{List X.} \\ &\quad \text{l } [\text{List X}] \\ &\quad (\lambda \text{h}: \text{X. } \lambda \text{t}: \text{List X. } \text{insert } [\text{X}] \text{ leq t h}) \\ &\quad (\text{nil } [\text{List X}]) \end{aligned} \)
章节23.5
练习23.5.1
题目:
If \( \Gamma \vdash \text{t}: \text{T} \) and \( \text{t} \rightarrow \text{t}' \), then \( \Gamma \vdash \text{t}': \text{T} \).
证明:
类似定理9.3.9的证明需要引理9.3.8一样,我们这里也需要一个类似的引理,如下:
引理1(Preservation of types under substitution):
If \( \Gamma, \text{x} : \text{S} \vdash \text{t}: \text{T} \) and \( \Gamma \vdash \text{s}: \text{S} \), then \( \Gamma \vdash [\text{x} \mapsto \text{s}] \text{t}: \text{T} \)
证明引理1:
使用结构归纳法,归纳假设命题对\( \text{t} \)的直接子项成立,我们要证明命题对\( \text{t} \)成立,对\( \text{t} \)的形式分情况进行讨论:
- 如果\( \text{t} = \text{true} \)或者\( \text{t} = \text{false} \),则\( \text{T} = \text{Bool} \),且不管在什么类型环境\( \Gamma \)下,均有\( \text{t}: \text{T} \),命题成立。
- 如果\( \text{t} = \text{if } \text{t}_1 \text{ then } \text{t}_2 \text{ else } \text{t}_3 \),则用Inversion引理(引理9.3.1,很简单,这里不证明了)可得, \( \Gamma, \text{x}: \text{S} \vdash \text{t}_1: \text{Bool} \quad \Gamma, \text{x}: \text{S} \vdash \text{t}_2: \text{T} \quad \Gamma, \text{x}: \text{S} \vdash \text{t}_3: \text{T} \),根据归纳假设,可得\( \Gamma \vdash [\text{x} \mapsto \text{s}] \text{t}_1: \text{Bool} \quad \Gamma \vdash [\text{x} \mapsto \text{s}] \text{t}_2: \text{T} \quad \Gamma \vdash [\text{x} \mapsto \text{s}] \text{t}_3: \text{T} \),进而根据T-IF,可得\( \Gamma \vdash [\text{x} \mapsto \text{s}] \text{t}: \text{T} \),命题成立。
- 如果\( \text{t} = \text{t}_1 \text{ } \text{t}_2 \),则可得\( \Gamma, \text{x}: \text{S} \vdash \text{t}_1: \text{T}_2 \to \text{T} \quad \Gamma, \text{x}: \text{S} \vdash \text{t}_2: \text{T}_2 \),根据归纳假设,可得\( \Gamma \vdash [\text{x} \mapsto \text{s}] \text{t}_1: \text{T}_2 \to \text{T} \quad \Gamma \vdash [\text{x} \mapsto \text{s}] \text{t}_2: \text{T}_2 \),进而根据T-APP,可得\( \Gamma \vdash [\text{x} \mapsto \text{s}] \text{t}: \text{T} \),命题成立。
- 如果\( \text{t} = \lambda \text{y}: \text{T}_2 \text{. } \text{t}_1 \),则可得\( \text{T} = \text{T}_2 \to \text{T}_1 \quad \Gamma, \text{x} : \text{S}, \text{y}: \text{T}_2 \vdash \text{t}_1: \text{T}_1 \),根据约定5.3.4,我们可以假设\( \text{x} \neq \text{y} \)且\( \text{y} \notin FV(\text{s}) \),由\( \Gamma, \text{x} : \text{S}, \text{y}: \text{T}_2 \vdash \text{t}_1: \text{T}_1 \),可得\( \Gamma, \text{y}: \text{T}_2, \text{x} : \text{S} \vdash \text{t}_1: \text{T}_1 \),此时根据归纳假设,可得\( \Gamma, \text{y}: \text{T}_2 \vdash [\text{x} \mapsto \text{s}] \text{t}_1: \text{T}_1 \),由\( \Gamma \vdash \text{s}: \text{S} \),可得\( \Gamma, \text{y}: \text{T}_2 \vdash \text{s}: \text{S} \),加上\( \Gamma, \text{y}: \text{T}_2 \vdash [\text{x} \mapsto \text{s}] \text{t}_1: \text{T}_1 \)以及T-ABS,可得\( \Gamma \vdash \lambda \text{y}: \text{T}_2 \text{. } [\text{x} \mapsto \text{s}] \text{t}_1: \text{T} \),也就是\( \Gamma \vdash [\text{x} \mapsto \text{s}] \text{t}: \text{T} \),命题成立。
- 如果\( \text{t} = \text{y} \),则\( \text{y}: \text{T} \in (\Gamma, \text{x}: \text{S}) \),分情况讨论:
- 如果\( \text{y} = \text{x} \),则\( \text{T} = \text{S}, [\text{x} \mapsto \text{s}] \text{t} = \text{s} \),而我们已经有\( \Gamma \vdash \text{s}: \text{S} \)了,可得\( \Gamma \vdash [\text{x} \mapsto \text{s}] \text{t}: (\text{S} = \text{T}) \),命题成立。
- 如果\( \text{y} \neq \text{x} \),则\( \text{y}: \text{T} \in \Gamma , [\text{x} \mapsto \text{s}] \text{t} = \text{t} = \text{y} \),再由\( \text{y}: \text{T} \in \Gamma \)以及T-VAR,可得\( \Gamma \vdash ([\text{x} \mapsto \text{s}] \text{t} = \text{t}): \text{T} \),命题成立。
- 如果\( \text{t} = \lambda \text{X. } \text{t}_1 \),则\( \text{T} = \forall \text{X. } \text{T}_1 \quad \Gamma, \text{x} : \text{S}, \text{X} \vdash \text{t}_1: \text{T}_1 \),由\( \Gamma, \text{x} : \text{S}, \text{X} \vdash \text{t}_1: \text{T}_1 \),可得\( \Gamma, \text{X}, \text{x} : \text{S} \vdash \text{t}_1: \text{T}_1 \),此时由归纳假设,可得\( \Gamma, \text{X} \vdash [\text{x} \mapsto \text{s}] \text{t}_1: \text{T}_1 \),再由T-TABS,可得\( \Gamma \vdash \lambda \text{X. } [\text{x} \mapsto \text{s}] \text{t}_1: \text{T} \),也就是\( \Gamma \vdash [\text{x} \mapsto \text{s}] \text{t}: \text{T} \),命题成立。
- 如果\( \text{t} = \text{t}_1 \text{ } [\text{T}_2] \),则\( \Gamma, \text{x}: \text{S} \vdash \text{t}_1: \forall \text{X. } \text{T}_1 \quad \text{T} = [\text{X} \mapsto \text{T}_2] \text{ } \text{T}_1 \),根据归纳假设,可得\( \Gamma \vdash [\text{x} \mapsto \text{s}] \text{t}_1: \forall \text{X. } \text{T}_1 \),进而根据T-TAPP,可得\( \Gamma \vdash ([\text{x} \mapsto \text{s}] \text{t}_1) \text{ } [\text{T}_2] : \text{T} \),也就是\( \Gamma \vdash [\text{x} \mapsto \text{s}] \text{t}: \text{T} \),命题成立。
综上,所有情况下命题都对\( \text{t} \)成立,归纳完毕。
证明引理1完毕。
还需要一个和引理1类似的,针对类型变量进行替换的引理,如下:
引理2(Preservation of types under type variable substitution):
If \( \Gamma, \text{X}, \Delta \vdash \text{t}: \text{T} \), then \( \Gamma, [\text{X} \mapsto \text{S}] \Delta \vdash [\text{X} \mapsto \text{S}] \text{t}: [\text{X} \mapsto \text{S}] \text{T} \).
这里需要允许额外附加类型环境\( \Delta \),不然我们等下我们对T-ABS以及T-TABS的情况进行讨论时,会用不了归纳假设。
需要注意的是: \( \text{S} \)内部如果包含类型变量,则它只能包含\( \Gamma \)中有的类型变量,而不能包含\( \text{X} \),或者\( \Delta \)中的类型变量,否则引理2会在T-TAPP的情况下失效,这似乎是求值规则和类型规则没有限制到的东西,我们这里直接隐式进行限制了。读者应该会觉得这个限制是自然的,因为没有这个限制的话,则当项\( \text{t} \)内部包含子项\( (\lambda \text{Y. } \text{t}_1) [\text{T}_1] \)的时候,会允许\( \text{T}_1 \)访问\( \text{t}_1 \)中引入的类型变量,但是这些类型变量的作用域范围不应该包括\( \text{T}_1 \)才对。
证明引理2:
使用结构归纳法,归纳假设命题对\( \text{t} \)的直接子项成立,我们要证明命题对\( \text{t} \)成立,对\( \text{t} \)的形式分情况进行讨论:
- 如果\( \text{t} = \text{true} \)或者\( \text{t} = \text{false} \),则\( \text{T} = \text{Bool} \),且不管在什么类型环境\( \Gamma \)下,均有\( \text{t}: \text{T} \),又\( [\text{X} \mapsto \text{S}] \text{t} = \text{t} \quad [\text{X} \mapsto \text{S}] \text{T} = [\text{X} \mapsto \text{S}] \text{Bool} = \text{Bool} = \text{T} \),可得\( \Gamma, [\text{X} \mapsto \text{S}] \Delta \vdash [\text{X} \mapsto \text{S}] \text{t}: [\text{X} \mapsto \text{S}] \text{T} \),命题成立。
- 如果\( \text{t} = \text{if } \text{t}_1 \text{ then } \text{t}_2 \text{ else } \text{t}_3 \),则可得\( \Gamma, \text{X}, \Delta \vdash \text{t}_1: \text{Bool} \quad \Gamma, \text{X}, \Delta \vdash \text{t}_2: \text{T} \quad \Gamma, \text{X}, \Delta \vdash \text{t}_3: \text{T} \),根据归纳假设,可得\( \Gamma, [\text{X} \mapsto \text{S}] \Delta \vdash [\text{X} \mapsto \text{S}] \text{t}_1: ([\text{X} \mapsto \text{S}] \text{Bool} = \text{Bool}) \quad \Gamma, [\text{X} \mapsto \text{S}] \Delta \vdash [\text{X} \mapsto \text{S}] \text{t}_2: [\text{X} \mapsto \text{S}] \text{T} \quad \Gamma, [\text{X} \mapsto \text{S}] \Delta \vdash [\text{X} \mapsto \text{S}] \text{t}_3: [\text{X} \mapsto \text{S}] \text{T} \),进而根据T-IF,可得\( \Gamma, [\text{X} \mapsto \text{S}] \Delta \vdash [\text{X} \mapsto \text{S}] \text{t}: [\text{X} \mapsto \text{S}] \text{T} \),命题成立。
- 如果\( \text{t} = \text{t}_1 \text{ } \text{t}_2 \),则可得\( \Gamma, \text{X}, \Delta \vdash \text{t}_1: \text{T}_2 \to \text{T} \quad \Gamma, \text{X}, \Delta \vdash \text{t}_2: \text{T}_2 \),根据归纳假设,可得\( \Gamma, [\text{X} \mapsto \text{S}] \Delta \vdash [\text{X} \mapsto \text{S}] \text{t}_1: [\text{X} \mapsto \text{S}] \text{T}_2 \to [\text{X} \mapsto \text{S}] \text{T} \quad \Gamma, [\text{X} \mapsto \text{S}] \Delta \vdash [\text{X} \mapsto \text{S}] \text{t}_2: [\text{X} \mapsto \text{S}] \text{T}_2 \),进而根据T-APP,可得\( \Gamma, [\text{X} \mapsto \text{S}] \Delta \vdash [\text{X} \mapsto \text{S}] \text{t}: [\text{X} \mapsto \text{S}] \text{T} \),命题成立。
- 如果\( \text{t} = \lambda \text{y}: \text{T}_2 \text{. } \text{t}_1 \),则可得\( \text{T} = \text{T}_2 \to \text{T}_1 \quad \Gamma, \text{X}, \Delta, \text{y}: \text{T}_2 \vdash \text{t}_1: \text{T}_1 \),注意到这里我们的附加类型环境派上用场了,这里\( \Delta, \text{y}: \text{T}_2 \)组成新的附加类型环境,根据归纳假设,可得\( \Gamma, [\text{X} \mapsto \text{S}] (\Delta, \text{y}: \text{T}_2) \vdash [\text{X} \mapsto \text{S}] \text{t}_1: [\text{X} \mapsto \text{S}] \text{T}_1 \),这相当于\( \Gamma, [\text{X} \mapsto \text{S}] \Delta, \text{y}: [\text{X} \mapsto \text{S}] \text{T}_2 \vdash [\text{X} \mapsto \text{S}] \text{t}_1: [\text{X} \mapsto \text{S}] \text{T}_1 \),根据T-ABS,可得\( \Gamma, [\text{X} \mapsto \text{S}] \Delta \vdash \lambda \text{y}: [\text{X} \mapsto \text{S}] \text{T}_2 \text{. } [\text{X} \mapsto \text{S}] \text{t}_1: [\text{X} \mapsto \text{S}] \text{T} \),也就是\( \Gamma, [\text{X} \mapsto \text{S}] \Delta \vdash [\text{X} \mapsto \text{S}] \text{t}: [\text{X} \mapsto \text{S}] \text{T} \),命题成立。
- 如果\( \text{t} = \text{y} \),则\( \text{y}: \text{T} \in (\Gamma, \text{X}, \Delta) \),可得\( \text{y}: \text{T} \in \Gamma \)或者\( \text{y}: \text{T} \in \Delta \),分情况讨论:
- 如果\( \text{y}: \text{T} \in \Gamma \),则类似约定5.3.4,我们所有引入类型环境中的类型变量的名称都是不同的,特别的,既然\( \Gamma, \text{X} \)是个合法的类型环境,则可得\( \text{X} \)不在\( \Gamma \)中,加上\( \text{y}: \text{T} \in \Gamma \),这意味着\( \text{T} \)中不包含\( \text{X} \),可得\( [\text{X} \mapsto \text{S}] \text{T} = \text{T} \),进而可得\( \text{y}: [\text{X} \mapsto \text{S}] \text{T} \in \Gamma \),于是根据T-VAR,有\( \Gamma, [\text{X} \mapsto \text{S}] \Delta \vdash ([\text{X} \mapsto \text{S}] \text{t} = [\text{X} \mapsto \text{S}] \text{y} = \text{y} = \text{t}): [\text{X} \mapsto \text{S}] \text{T} \),也就是\( \Gamma, [\text{X} \mapsto \text{S}] \Delta \vdash [\text{X} \mapsto \text{S}] \text{t}: [\text{X} \mapsto \text{S}] \text{T} \),命题成立。
- 如果\( \text{y}: \text{T} \in \Delta \),此时由于\( \Delta \)是在\( \text{X} \)类型变量后构建的类型环境,因此\( \Delta \)里面可能包含\( \text{X} \),而新的环境\( [\text{X} \mapsto \text{S}] \Delta \)把\( \Delta \)中所有的\( \text{X} \)都替换成\( \text{S} \)了,加上\( [\text{X} \mapsto \text{S}] \text{T} \)也把\( \text{T} \)中所有的\( \text{X} \)都替换成\( \text{S} \)了,易得\( \text{y}: [\text{X} \mapsto \text{S}] \text{T} \in [\text{X} \mapsto \text{S}] \Delta \),再根据T-VAR,可得\( \Gamma, [\text{X} \mapsto \text{S}] \Delta \vdash [\text{X} \mapsto \text{S}] \text{t}: [\text{X} \mapsto \text{S}] \text{T} \),命题成立。
- 如果\( \text{t} = \lambda \text{Y. } \text{t}_1 \),则\( \text{T} = \forall \text{Y. } \text{T}_1 \quad \Gamma, \text{X}, \Delta, \text{Y} \vdash \text{t}_1: \text{T}_1 \),由归纳假设,可得\( \Gamma, [\text{X} \mapsto \text{S}] (\Delta, \text{Y}) \vdash [\text{X} \mapsto \text{S}] \text{t}_1: [\text{X} \mapsto \text{S}] \text{T}_1 \),这等价于\( \Gamma, [\text{X} \mapsto \text{S}] \Delta, [\text{X} \mapsto \text{S}] \text{Y} \vdash [\text{X} \mapsto \text{S}] \text{t}_1: [\text{X} \mapsto \text{S}] \text{T}_1 \),而由约定可得\( \text{X} \neq \text{Y} \),进而可得\( [\text{X} \mapsto \text{S}] \text{Y} = \text{Y} \),综上可得\( \Gamma, [\text{X} \mapsto \text{S}] \Delta, \text{Y} \vdash [\text{X} \mapsto \text{S}] \text{t}_1: [\text{X} \mapsto \text{S}] \text{T}_1 \),再由T-TABS,可得\( \Gamma, [\text{X} \mapsto \text{S}] \Delta, \vdash \lambda \text{Y. } [\text{X} \mapsto \text{S}] \text{t}_1: \forall \text{Y. } [\text{X} \mapsto \text{S}] \text{T}_1 \),也就是\( \Gamma, [\text{X} \mapsto \text{S}] \Delta \vdash [\text{X} \mapsto \text{S}] \text{t}: [\text{X} \mapsto \text{S}] \text{T} \),命题成立。
- 如果\( \text{t} = \text{t}_1 \text{ } [\text{T}_2] \),则\( \Gamma, \text{X}, \Delta \vdash \text{t}_1: \forall \text{Y. } \text{T}_1 \quad \text{T} = [\text{Y} \mapsto \text{T}_2] \text{ } \text{T}_1 \),由\( \Gamma, \text{X}, \Delta \vdash \text{t}_1: \forall \text{Y. } \text{T}_1 \) 以及Inversion引理可得(我们前面有好几个地方用到了没明确说出来,这里比较重要,明确说下),可得\( \text{t}_1 = \lambda \text{Y. } \text{t}_2 \quad \Gamma, \text{X}, \Delta, \text{Y} \vdash \text{t}_2: \text{T}_1 \),这里既然\( \Gamma, \text{X}, \Delta, \text{Y} \)是合法的类型环境,由约定可得,\( \text{X} \neq \text{Y} \),再由\( \Gamma, \text{X}, \Delta \vdash \text{t}_1: \forall \text{Y. } \text{T}_1 \)以及归纳假设,可得\( \Gamma, [\text{X} \mapsto \text{S}] \Delta \vdash [\text{X} \mapsto \text{S}] \text{t}_1: \forall \text{Y. } [\text{X} \mapsto \text{S}] \text{T}_1 \),进而根据T-TAPP以及以\( [\text{X} \mapsto \text{S}] \text{T}_2 \)作为类型参数,可得\( \Gamma, [\text{X} \mapsto \text{S}] \Delta \vdash ([\text{X} \mapsto \text{S}] \text{t}_1) \text{ } [[\text{X} \mapsto \text{S}] \text{T}_2]: [\text{Y} \mapsto [\text{X} \mapsto \text{S}] \text{T}_2] ([\text{X} \mapsto \text{S}] \text{T}_1) \),这里把\( [\text{Y} \mapsto [\text{X} \mapsto \text{S}] \text{T}_2] ([\text{X} \mapsto \text{S}] \text{T}_1) \)换成 \( [\text{X} \mapsto \text{S}] ([\text{Y} \mapsto [\text{X} \mapsto \text{S}] \text{T}_2] \text{T}_1) \)是安全的,这是因为\( \text{Y} \)的替换类型\( [\text{X} \mapsto \text{S}] \text{T}_2 \)中已经不包含类型变量\( \text{X} \)了,进而把\( [\text{Y} \mapsto [\text{X} \mapsto \text{S}] \text{T}_2] \)移到\( [\text{X} \mapsto \text{S}] \)的作用范围内不会对\( [\text{Y} \mapsto [\text{X} \mapsto \text{S}] \text{T}_2] \)有影响,加上我们一开始讨论过的,限制\( \text{S} \)中包含的类型变量只能是\( \Gamma \)中有的类型变量,可得\( \text{S} \)不包含类型变量\( \text{Y} \),于是把\( [\text{X} \mapsto \text{S}] \)移到\( [\text{Y} \mapsto [\text{X} \mapsto \text{S}] \text{T}_2] \)的作用范围外也不会对\( [\text{X} \mapsto \text{S}] \)有影响,综上,可得\( \Gamma, [\text{X} \mapsto \text{S}] \Delta \vdash ([\text{X} \mapsto \text{S}] \text{t}_1) \text{ } [[\text{X} \mapsto \text{S}] \text{T}_2]: [\text{X} \mapsto \text{S}] ([\text{Y} \mapsto [\text{X} \mapsto \text{S}] \text{T}_2] \text{T}_1) \),也就是\( \Gamma, [\text{X} \mapsto \text{S}] \Delta \vdash [\text{X} \mapsto \text{S}] \text{t}: [\text{X} \mapsto \text{S}] \text{T} \),命题成立。
综上,所有情况下命题都对\( \text{t} \)成立,归纳完毕。
证明引理2完毕。
回去证明题目给的命题:
使用结构归纳法,归纳假设命题对\( \text{t} \)的直接子项成立,我们要证明命题对\( \text{t} \)成立,对\( \text{t} \)的形式分情况进行讨论:
- 首先,\( \text{t} \neq \text{true} \quad \text{false} \quad \lambda \text{x}: \text{T}_1 \text{. } \text{t}_1 \quad \lambda \text{X. } \text{t}_1 \quad \text{y} \),因为这几种形式下\( \text{t} \)为范式,和\( \text{t} \rightarrow \text{t}' \)矛盾。
- 如果\( \text{t} = \text{if } \text{t}_1 \text{ then } \text{t}_2 \text{ else } \text{t}_3 \),则可得\( \Gamma \vdash \text{t}_1: \text{Bool} \quad \Gamma \vdash \text{t}_2: \text{T} \quad \Gamma \vdash \text{t}_3: \text{T} \),分情况讨论:
- 如果\( \text{t}_1 = \text{true} \),则\( \text{t}' = \text{t}_2 \),可得\( \Gamma \vdash (\text{t}' = \text{t}_2): \text{T} \)。
- 如果\( \text{t}_1 = \text{false} \),则\( \text{t}' = \text{t}_3 \),可得\( \Gamma \vdash (\text{t}' = \text{t}_3): \text{T} \)。
- 如果\( \text{t}_1 \neq \text{true} \quad \text{false} \),则\( \text{t} \rightarrow \text{t}' \)能用的求值规则就只有E-IF了,可得\( \text{t}_1 \rightarrow \text{t}'_1, \text{t}' = \text{if } \text{t}'_1 \text{ then } \text{t}_2 \text{ else } \text{t}_3 \),由\( \text{t}_1 \rightarrow \text{t}'_1 \quad \Gamma \vdash \text{t}_1: \text{Bool} \)以及归纳假设,可得\( \Gamma \vdash \text{t}'_1: \text{Bool} \),进而T-IF,可得\( \Gamma \vdash \text{t}': \text{T} \)。
- 如果\( \text{t} = \text{t}_1 \text{ } \text{t}_2 \),则可得\( \Gamma \vdash \text{t}_1: \text{T}_2 \to \text{T} \quad \Gamma \vdash \text{t}_2: \text{T}_2 \),分情况讨论:
- 如果\( \text{t}_1 \)不为值,则\( \text{t} \rightarrow \text{t}' \)能使用的求值规则就只有E-APP1了,可得\( \text{t}_1 \rightarrow \text{t}'_1 \quad \text{t}' = \text{t}'_1 \text{ } \text{t}_2 \),由\( \text{t}_1 \rightarrow \text{t}'_1 \quad \Gamma \vdash \text{t}_1: \text{T}_2 \to \text{T} \)以及归纳假设,可得\( \Gamma \vdash \text{t}'_1: \text{T}_2 \to \text{T} \),进而根据T-APP,可得\( \Gamma \vdash \text{t}': \text{T} \)。
- 如果\( \text{t}_1 \)为值,则可得\( \text{t}_1 = \lambda \text{x}: \text{T}_2 \text{. } \text{t}_{11} \),分情况讨论:
- 如果\( \text{t}_2 \)不为值,则\( \text{t} \rightarrow \text{t}' \)能使用的求值规则就只有E-APP2了,可得\( \text{t}_2 \rightarrow \text{t}'_2 \quad \text{t}' = \text{t}_1 \text{ } \text{t}'_2 \),由\( \text{t}_2 \rightarrow \text{t}'_2 \quad \Gamma \vdash \text{t}_2: \text{T}_2 \)以及归纳假设,可得\( \Gamma \vdash \text{t}'_2: \text{T}_2 \),进而根据T-APP,可得\( \Gamma \vdash \text{t}': \text{T} \)。
- 如果\( \text{t}_2 \)为值,则\( \text{t} \rightarrow \text{t}' \)能使用的求值规则就只有E-APPABS了,可得\( \text{t}' = [\text{x} \mapsto \text{t}_2] \text{t}_{11} \),由\( \Gamma \vdash \text{t}_1: \text{T}_2 \to \text{T} \),可得 \( \Gamma, \text{x}: \text{T}_2 \vdash \text{t}_{11}: \text{T} \),加上\( \Gamma \vdash \text{t}_2: \text{T} \),根据引理1,可得\( \Gamma \vdash \text{t}': \text{T} \)。
- 如果\( \text{t} = \text{t}_1 \text{ } [\text{T}_2] \),则可得\( \Gamma \vdash \text{t}_1: \forall \text{X. } \text{T}_1
\quad \text{T} = [\text{X} \mapsto \text{T}_2] \text{T}_1 \),分情况讨论:
- 如果\( \text{t}_1 \)不为值,则\( \text{t} \rightarrow \text{t}' \)能使用的求值规则就只有E-TAPP了,可得\( \text{t}_1 \rightarrow \text{t}'_1 \quad \text{t}' = \text{t}'_1 \text{ } [\text{T}_2] \),由\( \text{t}_1 \rightarrow \text{t}'_1 \quad \Gamma \vdash \text{t}_1: \forall \text{X. } \text{T}_1 \)以及归纳假设,可得\( \Gamma \vdash \text{t}'_1: \forall \text{X. } \text{T}_1 \),进而根据T-TAPP,可得\( \Gamma \vdash \text{t}': \text{T} \)。
- 如果\( \text{t}_1 \)为值,则\( \text{t} \rightarrow \text{t}' \)能使用的求值规则就只有E-TAPPTABS了,可得\( \text{t}_1 = \lambda \text{X. } \text{t}_{11} \quad \Gamma, \text{X} \vdash \text{t}_{11}: \text{T}_1 \quad \text{t}' = [\text{X} \mapsto \text{T}_2] \text{ } \text{t}_{11} \),由\( \Gamma, \text{X} \vdash \text{t}_{11}: \text{T}_1 \)以及引理2,可得\( \Gamma \vdash [\text{X} \mapsto \text{T}_2] \text{ } \text{t}_{11}: [\text{X} \mapsto \text{T}_2] \text{ } \text{T}_1 \),也就是\( \Gamma \vdash \text{t}': \text{T} \)。
证毕。
练习23.5.2
题目:
If \( \text{t} \) is a closed, well-typed term, then either \( \text{t} \) is a value or else there is some \( \text{t}' \) with \( \text{t} \rightarrow \text{t}' \).
证明:
类似定理9.3.5的证明,我们也需要一个类似引理9.3.4的引理,如下:
引理1(CANONICAL FORMS):
- If \( \text{v} \) is a value of type \( \text{Bool} \), then \( \text{v} \) is either \( \text{true} \) or \( \text{false} \).
- If \( \text{v} \) is a value of type \( \text{T}_1 \to \text{T}_2 \), then \( \text{v} = \lambda \text{x}: \text{T}_1 \text{. } \text{t}_1 \).
- If \( \text{v} \) is a value of type \( \forall \text{X. } \text{T}_1 \), then \( \text{v} = \lambda \text{X. } \text{t}_1 \).
证明引理1:
从语法上来看,我们一共有如下形式的值:
- \( \text{true} \)
- \( \text{false} \)
- \( \lambda \text{x}: \text{T. } \text{t}_1 \)
- \( \lambda \text{X. } \text{t}_1 \)
如果\( \text{v} \)的类型是\( \text{Bool} \),则\( \text{true}, \text{false} \)两种值形式刚好是我们想要的,至于剩下的两种值形式\( \lambda \text{x}: \text{T. } \text{t}_1, \lambda \text{X. } \text{t}_1 \),根据Inversion引理,可得它们的类型不是\( \text{Bool} \),矛盾,故剩下的两种值形式是不可能的。综上,1是成立的。
如果\( \text{v} \)的类型是\( \text{T}_1 \to \text{T}_2 \),则值形式\( \lambda \text{x}: \text{T. } \text{t}_1 \)刚好是我们想要的,剩下的其他值形式同样根据Inversion引理,可得它们的类型不是\( \text{T}_1 \to \text{T}_2 \),矛盾,故剩下的其他值形式是不可能的。综上,2是成立的。
最后,3的证明和上面是类似的,易得3也成立。
证明引理1完毕。
现在回去证明题目给的命题:
使用结构归纳法,归纳假设命题对\( \text{t} \)的直接子项成立,我们要证明命题对\( \text{t} \)成立,对\( \text{t} \)的形式分情况进行讨论:
- 如果\( \text{t} \)为\( \text{true} \quad \text{false} \quad \lambda \text{x}: \text{T}_1 \text{. } \text{t}_1 \quad \lambda \text{X. } \text{t}_1 \)的其中一种形式,则直接有\( \text{t} \)为值,命题成立。
- \( \text{t} = \text{y} \)是不可能的,因为这意味着\( \text{t} \)不是闭合项。
- 如果\( \text{t} = \text{if } \text{t}_1 \text{ then } \text{t}_2 \text{ else } \text{t}_3 \),则由\( \text{t} \)是类型良好的,可得\( \Gamma \vdash \text{t}_1: \text{Bool}
\quad \Gamma \vdash \text{t}_2: \text{T} \quad \Gamma \vdash \text{t}_3: \text{T} \),
\( \text{t}_1, \text{t}_2, \text{t}_3 \)都是闭合项(不然\( \text{t} \)就不是闭合项了),根据归纳假设,可得\( \text{t}_1 \)要么是值,要么有\( \text{t}_1 \rightarrow \text{t}'_1 \),分情况讨论:
- 如果\( \text{t} \)是值,则\( \text{t}_1 = \text{true} \)或者\( \text{t}_1 = \text{false} \),两种情况下均可得\( \text{t} \rightarrow \text{t}' \),其中\( \text{t}' = \text{t}_2 \)或者\( \text{t}' = \text{t}_3 \),命题成立。
- 如果\( \text{t}_1 \)不是值,则有\( \text{t}_1 \rightarrow \text{t}'_1 \),进而根据E-IF,可得\( \text{t} \rightarrow \text{t}' \quad \text{t}' = \text{if } \text{t}'_1 \text{ then } \text{t}_2 \text{ else } \text{t}_3 \),命题成立。
- 如果\( \text{t} = \text{t}_1 \text{ } \text{t}_2 \),则由\( \text{t} \)是类型良好的,可得\( \Gamma \vdash \text{t}_1: \text{T}_2 \to \text{T}
\quad \Gamma \vdash \text{t}_2: \text{T}_2 \),它们都是闭合项,根据归纳假设,可得\( \text{t}_1 \)要么是值,要么有\( \text{t}_1 \rightarrow \text{t}'_1 \),同理也有\( \text{t}_2 \)要么是值,要么有\( \text{t}_2 \rightarrow \text{t}'_2 \),分情况讨论:
- 如果\( \text{t}_1 \)是值,则由引理1,可得\( \text{t}_1 = \lambda \text{x}: \text{T}_2 \text{. } \text{t}_{11} \),进一步分情况讨论:
- 如果\( \text{t}_2 \)是值,则由E-APPABS,可得\( \text{t} \rightarrow \text{t}' \quad \text{t}' = [\text{x} \mapsto \text{t}_2] \text{t}_{11} \),命题成立。
- 如果\( \text{t}_2 \)不是值,则有\( \text{t}_2 \rightarrow \text{t}'_2 \),此时根据E-APP2,可得\( \text{t} \rightarrow \text{t}' \quad \text{t}' = \text{t}_1 \text{ } \text{t}'_2 \),命题成立。
- 如果\( \text{t}_1 \)不是值,则有\( \text{t}_1 \rightarrow \text{t}'_1 \),此时根据E-APP1,可得\( \text{t} \rightarrow \text{t}' \quad \text{t}' = \text{t}'_1 \text{ } \text{t}_2 \),命题成立。
- 如果\( \text{t}_1 \)是值,则由引理1,可得\( \text{t}_1 = \lambda \text{x}: \text{T}_2 \text{. } \text{t}_{11} \),进一步分情况讨论:
- 如果\( \text{t} = \text{t}_1 \text{ } [\text{T}_2] \),则由\( \text{t} \)是类型良好的,可得\( \Gamma \vdash \text{t}_1: \forall \text{X. } \text{T}_1 \),
\( \text{t}_1 \)是闭合项,根据归纳假设,可得\( \text{t}_1 \)要么是值,要么有\( \text{t}_1 \rightarrow \text{t}'_1 \),分情况讨论:
- 如果\( \text{t}_1 \)是值,则由引理1,可得\( \text{t}_1 = \lambda \text{X. } \text{t}_{11} \),此时由E-TAPPTABS,可得\( \text{t} \rightarrow \text{t}' \quad \text{t}' = [\text{X} \mapsto \text{T}_2] \text{ } \text{t}_{11} \),命题成立。
- 如果\( \text{t}_1 \)不是值,则有\( \text{t}_1 \rightarrow \text{t}'_1 \),此时根据E-TAPP,可得\( \text{t} \rightarrow \text{t}' \quad \text{t}' = \text{t}'_1 \text{ } [\text{T}_2] \),命题成立。
证毕。
章节23.6
练习23.6.3
题目:
The normalization property implies that the untyped term \( \text{omega} = (\lambda \text{x. } \text{x x}) \text{ } (\lambda \text{y. } \text{y y}) \) cannot be typed in System F, since reduction of \( \text{omega} \) never reaches a normal form. However, it is possible to give a more direct, “combinatorial” proof of this fact, using just the rules defining the typing relation.
-
Let us call a System F term exposed if it is a variable, an abstraction \( \lambda \text{x}: \text{T. } \text{t} \), or an application \( \text{t s} \) (i.e., if it is not a type abstraction \( \lambda \text{X. } \text{t} \) or type application \( \text{t } [\text{S}] \)).
Show that if \( \text{t} \) is well typed (in some context) and \( \textit{erase}(\text{t}) = \text{m} \), then there is some exposed term \( \text{s} \) such that \( \textit{erase}(\text{s}) = \text{m} \) and \( \text{s} \) is well typed (possibly in a different context).
-
Write \( \lambda \overline{\text{X}} \text{. t} \) as shorthand for a nested sequence of type abstractions of the form \( \lambda \text{X}_1 \dots \lambda \text{X}_n \text{. t} \). Similarly, write \( \text{t} \text{ } [\overline{\text{A}}] \) for a nested sequence of type applications \( ((\text{t} \text{ } [\overline{\text{A}}]) \dots [\text{A}_{n - 1}]) \text{ } [\text{A}_n] \) and \( \forall \overline{\text{X}} \text{. T} \) for a nested sequence of polymorphic types \( \forall \text{X}_1 \dots \forall \text{X}_n \text{. T} \). Note that these sequences are allowed to be empty. For example, if \( \overline{\text{X}} \) is the empty sequence of type variables, then \( \forall \overline{\text{X}} \text{. T} \) is just \( \text{T} \).
Show that if \( \textit{erase}(\text{t}) = \text{m} \) and \( \Gamma \vdash \text{t}: \text{T} \), then there exists some \( \text{s} \) of the form \( \lambda \overline{\text{X}} \text{. } (\text{u } [\overline{\text{A}}]) \), for some sequence of type variables \( \overline{\text{X}} \), some sequence of types \( \overline{\text{A}} \), and some exposed term \( \text{u} \), with \( \textit{erase}(\text{s}) = \text{m} \) and \( \Gamma \vdash \text{s}: \text{T} \).
-
Show that if \( \text{t} \) is an exposed term of type \( \text{T} \) (under \( \Gamma \)) and \( \textit{erase}(\text{t}) = \text{m n} \), then \( \text{t} \) has the form \( \text{s u} \) for some terms \( \text{s} \) and \( \text{u} \) such that \( \textit{erase}(\text{s}) = \text{m} \) and \( \textit{erase}(\text{u}) = \text{n} \), with \( \Gamma \vdash \text{s}: \text{U} \to \text{T} \) and \( \Gamma \vdash \text{u}: \text{U} \).
-
Suppose \( \text{x}: \text{T} \in \Gamma \). Show that if \( \Gamma \vdash \text{u}: \text{U} \) and \( \textit{erase}(\text{u}) = \text{x x} \), then either
- \( \text{T} = \forall \overline{\text{X}} \text{. } \text{X}_i \), where \( \text{X}_i \in \overline{\text{X}} \) or else
- \( \text{T} = \forall \overline{\text{X}}_1 \overline{\text{X}}_2 \text{. } \text{T}_1 \to \text{T}_2 \), where \( [\overline{\text{X}}_1 \overline{\text{X}}_2 \mapsto \overline{\text{A}}] \text{T}_1 = [\overline{\text{X}}_1 \mapsto \overline{\text{B}}](\forall \overline{\text{Z}} \text{. } \text{T}_1 \to \text{T}_2) \) for some sequences of types \( \overline{\text{A}} \) and \( \overline{\text{B}} \) with \( |\overline{\text{A}}| = |\overline{\text{X}}_1 \overline{\text{X}}_2| \) and \( |\overline{\text{B}}| = |\overline{\text{X}}_1| \).
-
Show that if \( \textit{erase}(\text{s}) = \lambda \text{x. m} \) and \( \Gamma \vdash \text{s}: \text{S} \), then \( \text{S} \) has the form \( \forall \overline{\text{X}} \text{. } \text{S}_1 \to \text{S}_2 \), for some \( \overline{\text{X}}, \text{S}_1 \), and \( \text{S}_2 \).
-
Define the leftmost leaf of a type \( \text{T} \) as follows: \[ \begin{aligned} \textit{leftmost-leaf}(\text{X}) &= \text{X} \\ \textit{leftmost-leaf}(\text{S} \to \text{T}) &= \textit{leftmost-leaf}(\text{S}) \\ \textit{leftmost-leaf}(\forall \text{X. } \text{S}) &= \textit{leftmost-leaf}(\text{S}). \end{aligned} \] Show that if \( [\overline{\text{X}}_1 \overline{\text{X}}_2 \mapsto \overline{\text{A}}] (\forall \overline{\text{Y}} \text{. } \text{T}_1) = [\overline{\text{X}}_1 \mapsto \overline{\text{B}}] (\forall \overline{\text{Z}} \text{. } (\forall \overline{\text{Y}} \text{. } \text{T}_1) \to \text{T}_2) \), then it must be the case that \( \textit{leftmost-leaf}(\text{T}_1) = \text{X}_i \) for some \( \text{X}_i \in \overline{\text{X}}_1 \overline{\text{X}}_2 \).
-
Show that \( \text{omega} \) is not typable in System F.
证明:
有难度+费时,跳过。
章节23.7
练习23.7.1
题目:
Translate the unsound example on page 335 into System F extended with references (Figure 13-1).
第335页中不安全的例子:
\( \begin{aligned} &\text{let r } = \text{ref } (\lambda \text{x. x}) \text{ in} \\ &(\text{r} := (\lambda \text{x}: \text{Nat. } \text{succ x}); (!\text{r}) \text{ } \text{true}); \end{aligned} \)
Figure 13-1:
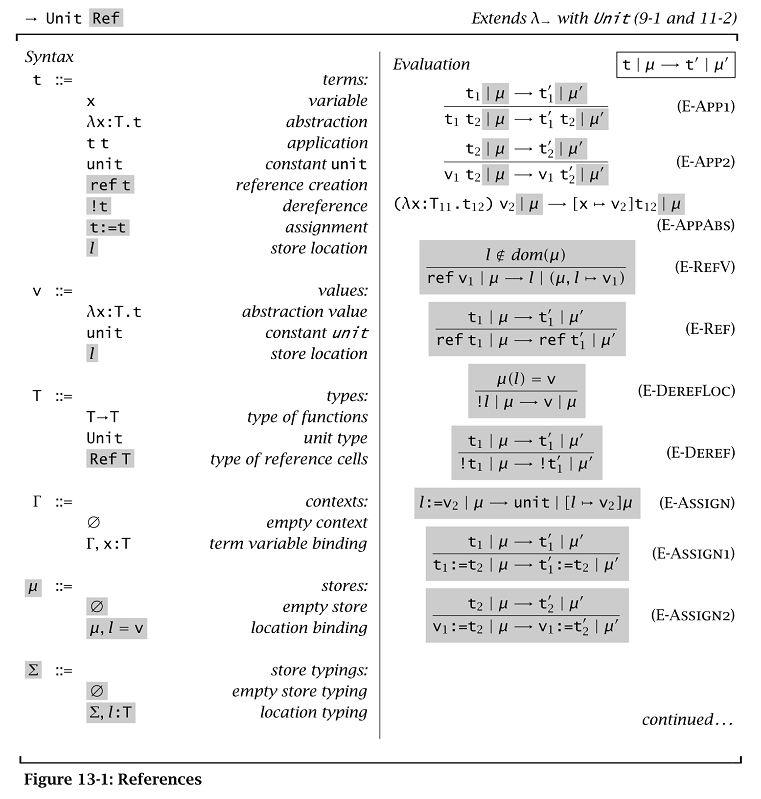
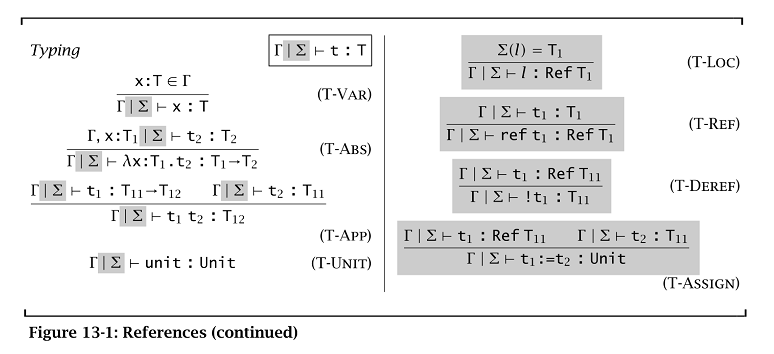
解答:
在上述不安全的例子中,\( \lambda \text{x. x} \)的类型是未限定的(多态的),不同的使用方式会推导出不同的类型,在System F下,我们直接引入一个类型变量给它用即可,当然,我们还得在合适的地方加上类型变量参数的实例化,如下:
\( \begin{aligned} \text{let r } = &\text{ }\lambda \text{X. } \text{ref } (\lambda \text{x}: \text{X. x}) \text{ in} \\ &\quad (\text{r} \text{ } [\text{Nat}] := (\lambda \text{x}: \text{Nat. } \text{succ x}); (!(\text{r} \text{ } [\text{Bool}])) \text{ } \text{true}); \end{aligned} \)
可以看到,该不安全的例子在System F下仍然是类型良好的,但是语义也仍然还是有问题的(求值过程仍然会出问题)。